Misc
Math Learning Center
Now open.
Hours are roughly Monday through Thursday mid-day and evening, Sunday evening.
See https://www.geneseo.edu/math/mlc for details.
This week is “open house week” w/ free snacks, etc.
Google Calendar
Demonstrate how to make appointments with me through it.
Also see this video from CIT:
Questions?
Cylinders
Definition
Does the shape you informally call a “cylinder” meet the mathematical definition of “cylinder”? If so, explain how. Give some examples of its rulings, and say what curve they pass through and what line they’re parallel to.
Yes, because a mathematical cylinder is the shape produced by pushing any curve along a set of parallel lines:
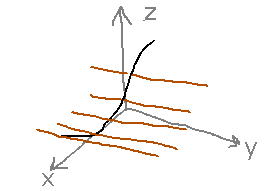
In the case of an informal cylinder, the curve is a circle and the lines are perpendicular to that circle. The rulings are lines along the length of the informal cylinder:
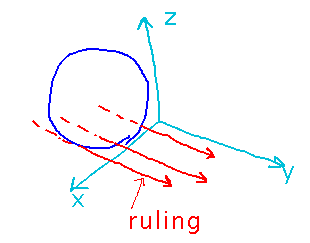
Example
Find an equation for the cylinder that passes through the curve z = y2 when x = 0, rising as x increases, at a 45 degree angle. Here’s a sketch of part of the cylinder, with parabolic cross-sections (traces) parallel to the yz plane and rising as x increases:
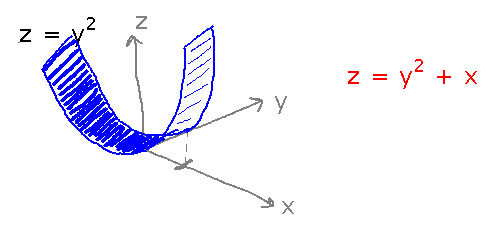
Equation z = y2 + x seems like it ought to work.
Plot this equation to see if it looks like you intended.
It does — see the Mathematica commands and results here. Notice a new Mathematica plotting command Plot3D, which is a little simpler for plotting surfaces on which z is an explicit function of x and y. Also notice the BoxRatios option to plotting commands to adjust the relative screen lengths of a plot’s axes.
Key Points
Further experience with 3D coordinates and plotting and Mathematica
Next
Cylindrical and spherical coordinates
Read section 2.7