
SUNY Geneseo Department of Mathematics
Thursday, May 2
Math 221 03
Spring 2019
Prof. Doug Baldwin
Thursday, May 9 (study day)
1:00 - 2:00
In our regular classroom (Sturges 221).
Bring things you want to talk about.
Please fill out the survey re when you would like the last SI session to be.
Thursday, May 16, 12:00 Noon.
Comprehensive, but emphasizing material since 2nd hour exam (e.g., Mean Value Theorem, limits at infinity, Riemann sums, definite integrals, substitution, applications of integration; roughly problem sets 7 through 9).
Rules and format otherwise similar to hour exams, especially open-references rule.
Designed for about 2 hours, you’ll have 3 hours 20 minutes
I’m working on practice questions.
I’ll bring donuts and cider.
SOFIs are under way.
Please fill them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).
Find the integral from 1 to 2 of x(x2-1)3.
Start with a substitution. So find a way of rewriting the integrand in terms of u and du.

This example was particularly tricky to decompose into u and du. Another way to think about substitution is that it reverses the chain rule, i.e., it’s how you find an antiderivative to a derivative that was taken using the chain rule. Specifically, using the chain rule on f(g(x)) produces f′(g(x)) g′(x). So if you can recognize something you’re trying to integrate as having the form f′(g(x)) g′(x), you know the antiderivative is f(g(x)). This is what we’ve been doing, but we called g(x) u, and g′(x) du.
However you do it, once you find the substitution, you can take an antiderivative. But since this is a definite integral with bounds, there’s a way you can save yourself some work: the bounds are actually x values, so convert them to u. Then you can take an antiderivative in terms of u, and evaluate it at the upper and lower u bounds, without ever having to undo the substitution like we did for indefinite integrals.
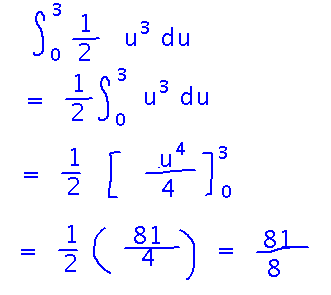
Here’s the above example in single figure, as it appeared when we finished it in class:

Another example: find the integral from π to 2π of (sinx + 10) cosx. Do this by substitution, including expressing the bounds in terms of u. But when you do that, both bounds turn out to be the same, which immediately means the integral is 0. This is an extreme example of how converting bounds when using substitution in a definite integral can save you lots of work.
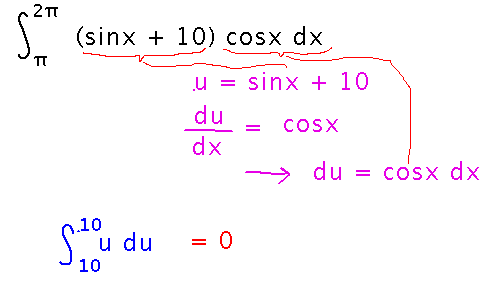
Notice that instead of expressing the bounds in terms of u, you can get the same result by keeping the bounds in terms of x, undoing the substitution after finding the antiderivative, and then plugging the original bounds into the antiderivative:
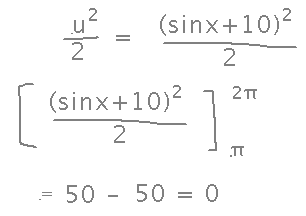
But notice that this was more work, and therefore more places to make mistakes, than working with the bounds in terms of u.
Here’s the above example in a single picture, as it finished in class:
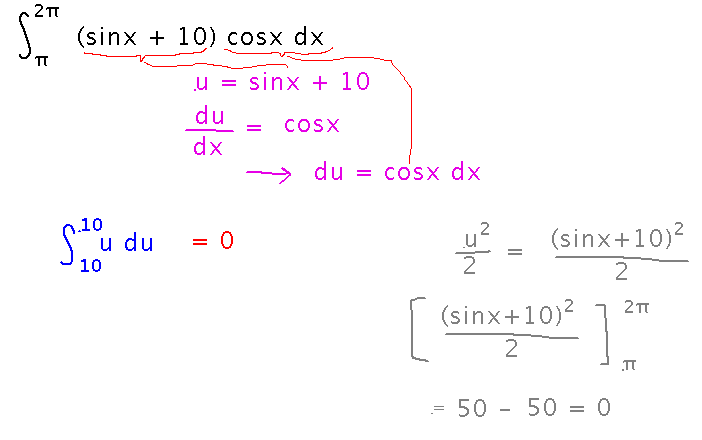
When evaluating a definite integral by substitution, express the bounds in terms of u to save a little work later.
Applications of integration: subtleties with area
Example: what is the area between the graph of y = x3 and the x axis between x = -1 and 1?
Read “Area and the Definite Integral” in section 5.2 if you haven’t already.