Misc
Colloquium
Prof. Cesar Aguilar
Examples in Analysis
Thursday, May 2, 2:30, Welles 138
Aimed at people with calculus 2, but give it a try if you want.
Extra credit for reactions/connections/reflection paragraph.
Review Session
Thursday, May 9 (study day)
1:00 - 2:00
In our regular classroom (Sturges 221).
Bring things you want to talk about.
SI
This afternoon.
Last SI session next Wednesday will be double length. Please fill out survey re when you would like it to be.
Final Exam
Thursday, May 16, 12:00 Noon.
Comprehensive, but emphasizing material since 2nd hour exam (e.g., Mean Value Theorem, limits at infinity, Riemann sums, definite integrals, substitution, applications of integration; roughly problem sets 7 through 9).
Rules and format otherwise similar to hour exams, especially open-references rule.
Designed for about 2 hours, you’ll have 3 hours 20 minutes
I’m working on practice questions.
I’ll bring donuts and cider.
SOFIs
SOFIs have started!
Please fill them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).
Questions?
Integration by Substitution
Section 5.5.
Example
Find the antiderivatives of (2x-2) √(x2-2x)
Start with pattern-matching, i.e., look for any part of the integrand whose derivative you spot in another part. Once you substitute u and du into the integral you can’t be left with any occurrences of x, but the substitution doesn’t have to produce just “u du” as the integrand, it can produce some function of u.
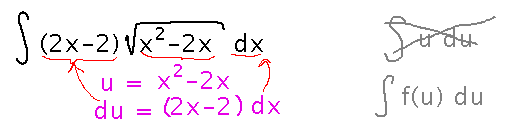
Once you identify u, write the integral in terms of it and integrate. In this case the key integration rule is the antiderivative power rule.
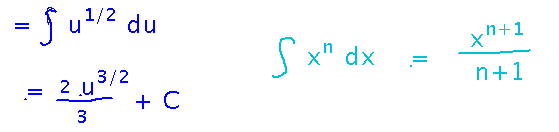
Finally, undo the substitution by replacing u with the original expression(s) involving x:
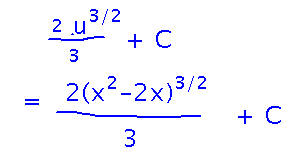
Here’s the complete solution as it looked when we finished doing it:
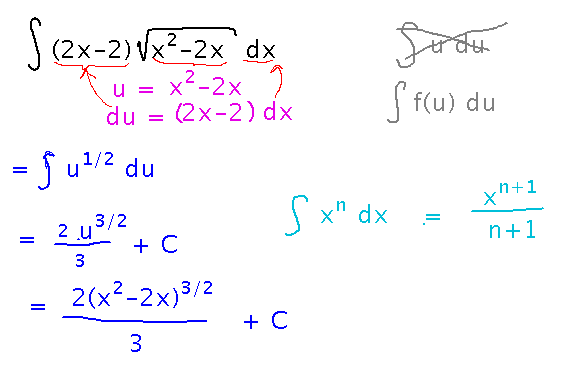
Alteration
What about antiderivatives of (x-1) √(x2-2x)?
The idea here is that you don’t need to match du exactly, if you can match a multiple of it you can multiply the integrand by the appropriate factor to make a match.
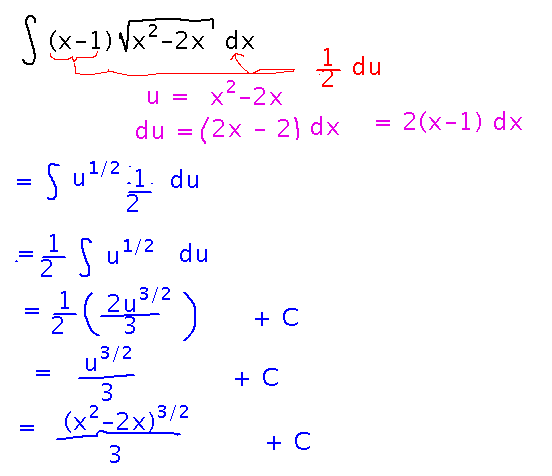
How about antiderivatives of sin(x/7)?
This time we considered several possible substitutions before finding one that worked. Once again, we needed to multiply by a constant to make the match.
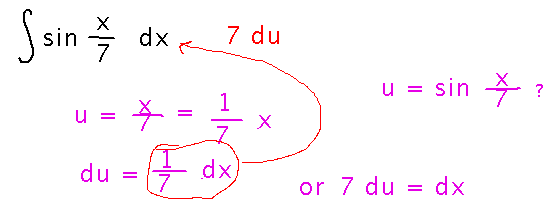
Once we finally found the right substitution, we could integrate:
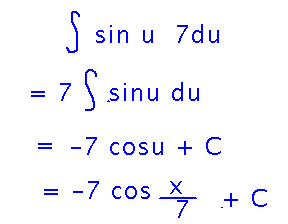
Here’s the complete solution, as it looked when we finished:
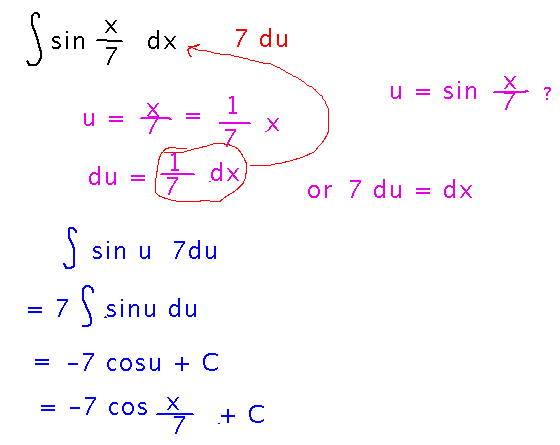
Key Points
Finding u and du is a matter of spotting patterns, it can take practice.
If your integrand contains a multiple of du, say c du for some constant c, you can still make substitution work by multiplying the integrand by 1/c. (Another way to think of this is that dx in the original integral is 1/c du, and so gets replaced by that expression when doing the substitution.)
Next
More practice with substitution, especially when it appears in definite integrals.