Misc
“Town Hall” re Bias Incidents
Tuesday (tomorrow) 5:00 - 8:00 PM, Macvittie Ballroom.
Hosted by student group Activists Fighting Racial Oppression (AFRO).
RSVP by 10:00 AM Tuesday at https://docs.google.com/forms/d/e/1FAIpQLScATpC6NTbGh3LDd_gfYHzGTvZOGrMX3pN1kO1oh-h1Upu5qA/viewform?usp=sf_link
Final Exam
Thursday, May 16, 12:00 Noon.
Comprehensive, but emphasizing material since 2nd hour exam (e.g., Mean Value Theorem, limits at infinity, Riemann sums, definite integrals, substitution, applications of integration; roughly problem sets 7 through 9).
Rules and format otherwise similar to hour exams, especially open-references rule.
Designed for about 2 hours, you’ll have 3 hours 20 minutes
I’ll put together some practice questions.
I’ll bring donuts and cider.
Would you like a roughly 1 hour review session on study day? Yes!
SOFIs
SOFIs have started!
Please fill them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).
Questions?
Breaking sums into parts? One way to do this is to break a sum that contains a sum or difference of two terms into a sum or difference of the sums of each term. For example...
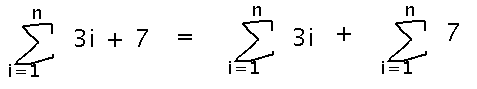
But there’s not an analogous way to break up a product inside a sum. In such cases, you have to hope you can algebraically rewrite the product into something you can work with. For example...
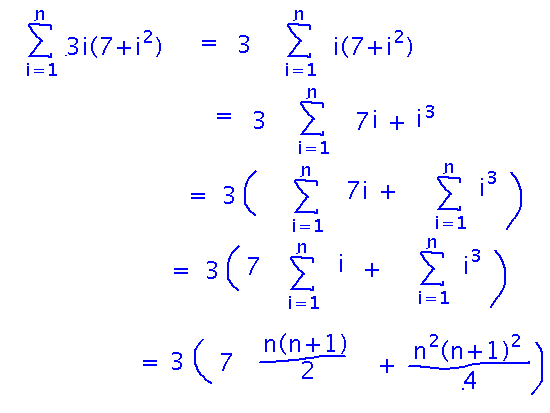
Definite Integrals with Mathematica
Use the Integrate function with a range of values for the variable.
This notebook demonstrates both a definite integral and an antiderivative. (And how to use Mathematica to quickly look something up, in this case the closed form for the sum from 1 to n of i3.)
Integration by Substitution
Section 5.5
Basic Idea
What is the antiderivative of sin2x cosx?
What does it have to do with the reading?
U-substitution: similar to the chain rule for taking derivatives, u-substitution lets you find antiderivatives in certain cases where an outer function is applied to an inner one. (In fact u-substitution is exactly the inverse of the chain rule, i.e., it finds antiderivatives that would then need the chain rule in order to be differentiated.)
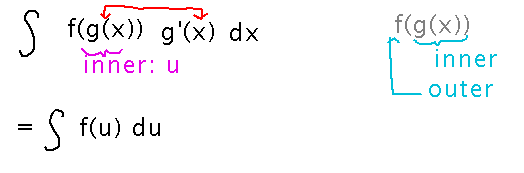
But the limit to when you can use substitution is that in addition to having an inner function g(x), you also have to have its derivative, g′(x). This is because in substitution you want to replace dx with du as well as replacing expressions involving x with ones involving u:
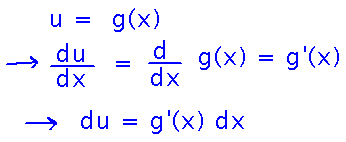
The whole u-substitution idea as it appeared in class is...
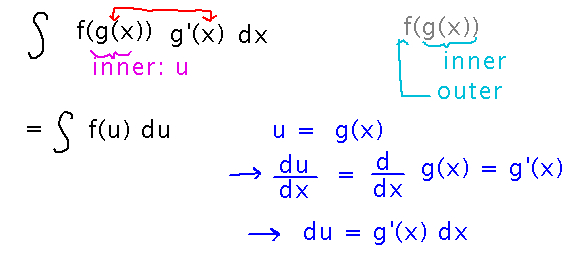
Try applying this to the sin2x cosx example. Start by identifying u and its derivative:

Then express the problem in terms of u and apply antiderivative rules:
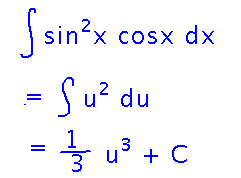
Finally, replace u with its definition in terms of x:
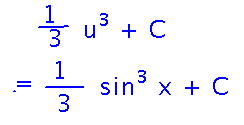
And here’s the whole substitution example as it looked at the end of our discussion in class:
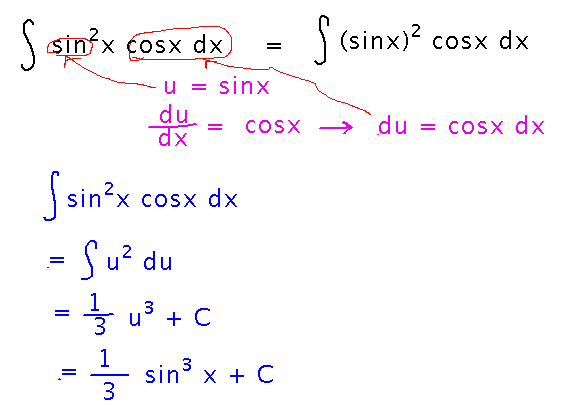
Key Points
Substitution is a technique for finding antiderivatives when there is an outer function, and an inner function with its derivative.
Next
More examples of substitution.
Read section 5.5 if you haven’t already.