Geneseo Math 221 03 Fundamental Theorem 2

Misc

SOFIs

SOFIs have started!

Please fill them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).

SI

This afternoon, 3:00, Bailey 209.

Questions?

What is the distinction between the terms “antiderivative” and “integral”?

Antiderivative of f: anything whose derivative is f
(Definite) integral of f: limit of a Riemann sum of f(x) over a certain range of x values
Indefinite integral of f: antiderivative of f

The Fundamental Theorem of Calculus, Part 2

Last part of section 5.3.

Example

Evaluate a definite integral.

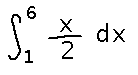
Integral from 1 to 6 of x over 2

What does this have to do with the reading?

According to the reading, you can evaluate definite integrals by finding an antiderivative of the integrand, evaluating it at the upper and lower bounds of the integral, and subtracting.

Simplify to 1 half times integral of x, antiderivative is x squared over 2, evaluate at 6 and 1 and subtract

A Catalog of Antiderivative Rules

(Particularly useful now that antiderivatives let you evaluate definite integrals without working through a Riemann sum.)

Sum/Difference Rule

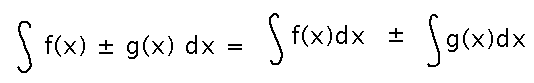
Integral of f plus or minus g is integral of f plus integral of g

Constant Multiple Rule

Integral of constant times f is that constant times integral of f

Power Rule

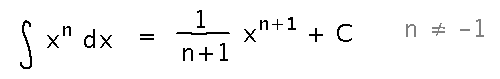
Integral of x to the n is 1 over n plus 1 times x to the n plus 1 (plus a constant)

Common Trigonometric Antiderivatives

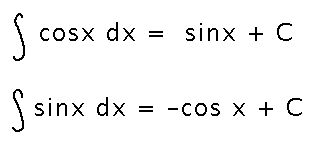
Integral of cosine is sine, integral of sine is negative cosine

...And here’s the whole table at once:

Sum, difference, constant multiple, power, and trig antiderivative rules

Note that similar but much bigger tables appear in the backs of textbooks, online, etc.

Another Fundamental Theorem Example

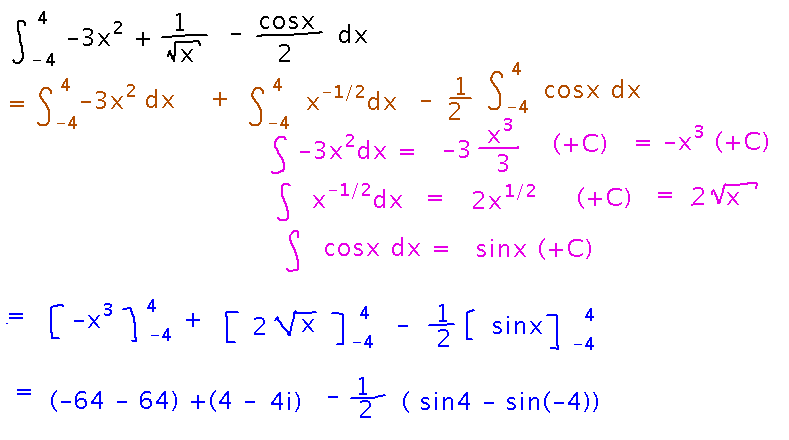
Evaluating integral from minus 4 to 4 of minus 3 x squared plus 1 over square root of x minus cosine x over 2

As with the first example, do this by simplifying the definite integral where you can and want to, then find antiderivatives, and finally evaluate them at the upper and lower bounds and subtract.

(Normally problems in this course won’t involve imaginary numbers, hopefully the imaginary part of this answer isn’t confusing. Elsewhere in this course, and particularly in sums, “i” is just an ordinary variable.)

Key Points

Process for evaluating a definite integral:

Simplify the integral (optional)
Find an antiderivative
Evaluate the antiderivative at the upper and lower bounds of the integral and subtract

Antiderivative rules and using them.

Suppose you wanted to find the antiderivatives of sin²x cosx. How would you do it? (Anti-hint: we don’t have a product rule for antiderivatives.)

Read section 5.5 on substitution.