SUNY Geneseo Department of Mathematics

Properties of Integrals

Wednesday, April 24

Math 221 03
Spring 2019
Prof. Doug Baldwin

Questions?

What to do with a sum that doesn’t start at 1, as in question 1 part B of problem set 8?

Use the property that a sum over a large range can be split into a sum of sums that collectively cover the entire range:

Sum from 1 to n splits into sum from 1 to b plus sum from b plus 1 to n

Properties of Integrals

Recall our calculation Monday that the integral from 0 to 2 of x³ is 4, and the book’s calculation that the integral from 0 to 2 of x² is 8/3.

So what is the integral from 0 to 2 of x³ + x²?

Use the property that an integral of a sum (or difference) can be broken into a sum (or difference) of two integrals to evaluate this as two integrals we already know:

Integral of sum of 2 functions is sum of integrals of each function

What about the integral of 5x³?

Another useful property: the integral of a constant times f(x) is the constant times the integral of f(x). Notice that this property, and the previous one, both come from the corresponding properties of sums and the fact that a definite integral really is a sum.

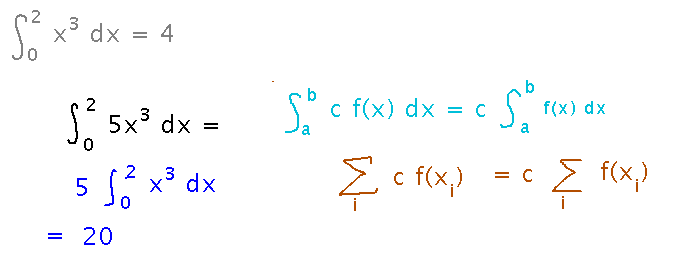
Integral of constant times f is the constant times integral of f

What do you suppose the integral from 2 to 0 of x³ is?

You can also analyze this in terms of integrals as sums. The key idea is that integrating from b to a instead of a to b changes the sign of Δx, and thus the sign of the integral:

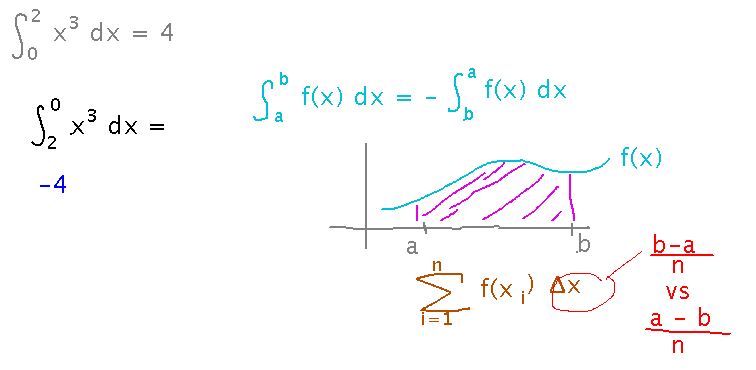
Delta x becomes a minus b over n instead of b minus a over n

What about the integral from 0 to 0 of x³?

If you integrate over an interval of length 0, Δx becomes 0, and so the integral is 0:

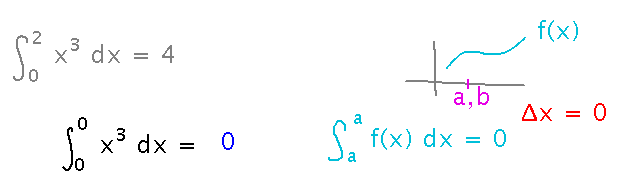
Integral over zero-width interval is 0

Fact: the integral from 0 to 1 of x³ is 1/4. What is the integral from 1 to 2 of x³?

Since sums over a range of values can be split into multiple sums that each cover part of the range, and integrals are sums, an integral over interval a to b can be split into a sum of integrals whose bounds collectively cover the interval a to b:

Integral from a to b can split into integral from a to c plus integral from c to b

Riemann Sums in Surprising Places

Suppose you have a function f(x), and an interval of x values a ≤ x ≤ b. What’s the average value of f(x) over that interval?

If we had, say, 2 values of the function, we could calculate the average easily:

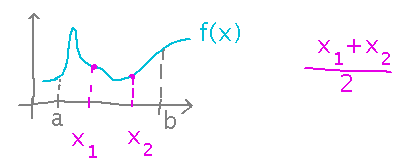
Function sampled at x1 and x2 has average value f of x1 plus f of x2 over 2

But this isn’t very accurate, because those 2 values likely miss lots of interesting peaks and dips in the function. So use more samples, say n of them, spaced some constant amount, say Δx, apart.

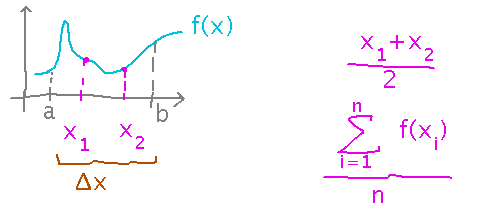
Average of n samples is sum from 1 to n of sample values divided by n

Now we can calculate Δx just like we did for calculating area. From that, we can express n in terms of Δx, and use that definition of n in the formula for the average:

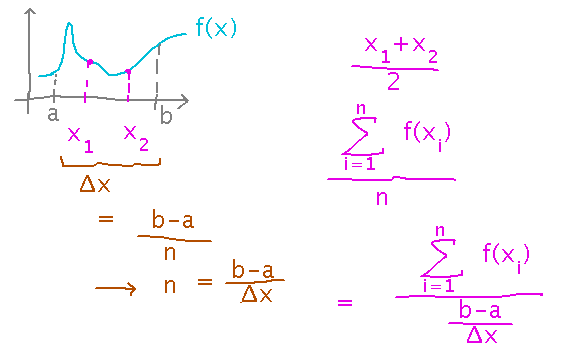
Delta x equals b minus a over n, so n equals b minus a over Delta x

And we can simplify this to not have a fraction in the denominator:

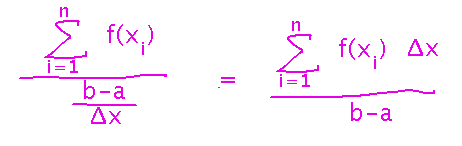
Average is sum of function values times Delta x all over b minus a

But now the numerator in the average is a Riemann sum! And in fact, the more samples of the function we have, i.e., the bigger n is, the more accurate the average. So to get an exact average, take the limit of the sum as n goes to infinity, and lo and behold the average turns out to be calculable as an integral:

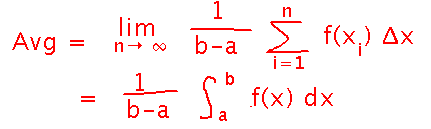
Average is integral from a to b of f times 1 over b minus a

Key Points

Integrals have algebraic properties.

Use those properties to avoid calculating Riemann sums.

We’ll see a lot of non-obvious places where Riemann sums, and thus definite integrals, turn up — average value of a function was just the first.

The Fundamental Theorem of Calculus, Part 1.

Read the introduction, “The Mean Value Theorem for Integrals”, and “Fundamental Theorem of Calculus Part 1: Integrals and Antiderivatives” in section 5.3.

Next Lecture