Areas Under Curves

Return to Course Outline

Previous Lecture

Misc

GREAT Day

Wednesday (April 17).

Lots of math talks and posters; go see them (and other things, too).

Extra credit for writing reactions/reflection on any one math-related presentation.

Colloquium

Dr. Stephanie Singer (also the GREAT Day keynote speaker)

“Defending Democracy with Mathematics”

Thursday, April 18, 2:30 - 3:30

Welles 138

Extra credit for written reactions/reflections, as usual.

Society of Actuaries Visit

An opportunity to learn something about actuarial careers.

Thursday, April 18, 3:45 PM.

South 336.

Questions?

Area Under the Graph of a Function

Section 5.1

What’s the basic idea?

Approximate the smooth-edged area under a graph with a series of rectangles. As the rectangles get thinner, they hug the graph more closely and give a better estimate of the area.

Summations

An important preliminary

Concrete Example

Calculate the sum from 1 to 4 of i.

You could expand the sum into an explicit addition of terms, and get 10:

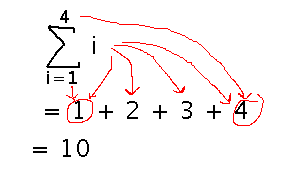
Is your result consistent with the general rule that the sum from 1 to n of i is n(n+1)/2? It is: n stands for the upper bound in the general rule, so plug 4 in for n to apply this “closed form” to our problem:

Here are the above two calculations side-by-side as they appeared in class:

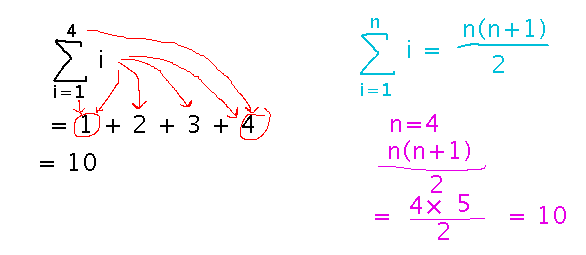
You can also do sums and evaluate closed form formulas in Mathematica. The Sum function is key to evaluating sums in Mathematica. This notebook demonstrates some examples.

A More Abstract Example

What is the sum of the first n odd numbers?

Notice that...

• The first odd number is 1 which can be written as 2 × 1 - 1
• The second odd number is 3 which can be written 2 × 2 - 1
• The third odd number is 5 which can be written 2 × 3 - 1
• In general, the k^th odd number is 2k - 1

Use algebraic rules for summations (e.g., that they can be split into separate sums at addition or subtraction operations, constant multiples can be factored out of them) and known closed forms (e.g., for the sum of the first n whole numbers, or the sum of a constant) to simplify:

Areas under Graphs

Approximate the area under the graph of y = x between x = 1 and x = 3 as a series of rectangles.

Strategy: Do an example of area as rectangles explicitly, calculating and adding up areas. Then see if we can find a summation formula for the area as the number of rectangles increases, and simplify it into a formula that doesn’t require explicitly adding things up.

Notice that the actual area can be computed exactly thanks to geometry. This gives us an exact answer to compare the sums-of-rectangles areas to. For example, the area between x = 1 and x = 3 and under the line y = x is the area of the triangle from x = 0 to x = 3 and under the line minus the area of the triangle from x = 0 to x = 1:

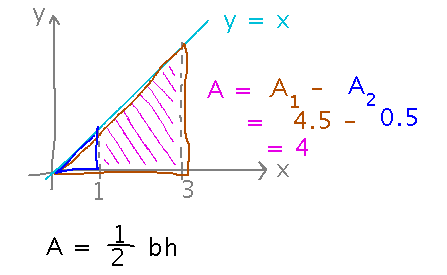
Key Points

The idea of summing many numbers, sigma notation.

Algebra of sums and closed forms can be used to simplify/calculate with sums.

Next

Thursday — no class Wednesday.

Definite integrals as Riemann sums (including the area under y = x started above)

Read introduction and “Definition and Notation” subsections of section 5.2.

Next Lecture