SUNY Geneseo Department of Mathematics

The Chain Rule, Part 1

Monday, February 25

Math 221 03
Spring 2019
Prof. Doug Baldwin

Misc

I will be out of town at a conference Thursday and Friday this week. Instead of face-to-face class meetings, we will do online discussions I can be part of while traveling. SI will meet as usual.

Bring laptops on Wednesday

Questions?

Problem Set Question 3

How to approach the question?

Recall that a derivative is essentially a slope, so visually judge where the slope of the curve is positive, negative, etc.

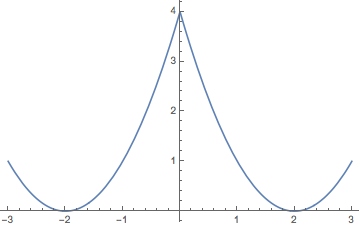
Side-by-side parabolas opening upward and meeting at a peak at x equals 0

What about the part of question that requires explaining why the derivative is undefined at x = 0?

The derivative is discontinuous at x = 0, and you can support that claim either visually or a little more theoretically. Visually, the slope of the curve is positive, and in fact increasingly so, on one side of x = 0, but increasingly negative on the other, so the derivative must jump from positive to negative at x = 0. More theoretically, if you imagine evaluating the derivative as a limit at x = 0, positive values of h will produce a negative derivative, while negative h will produce a positive derivative, i.e., the one-sided limits of (f(x+h) - f(x))/h as h approaches 0 differ.

Question 1 Part 2

The limit definition of derivative produces a numerator of (x+h)/(x+h+1) - x/(x+1). Now what to do?

Try putting both parts of this expression over a common denominator, and see if the entire limit expression simplifies.

Deriving the Constant Rule

What does f(x+h) become in this derivation?

The trick is to realize what it means to say that f(x) = c:

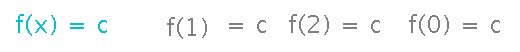
f of x equals c means f is c when x is 1, 2, 0, etc.

In particular, f(x+h) is also c, no matter what x and h are. The limit is then straightforward to evaluate:

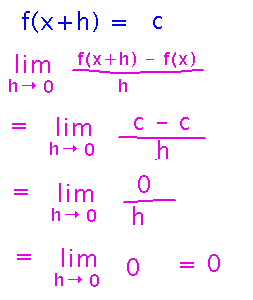
Derivative of a constant as a limit simplifies to a limit as h approaches 0 of 0 over h

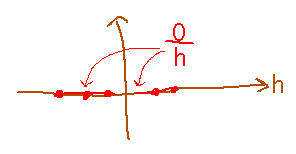
Notice that even though plugging h = 0 into 0/h would be undefined, that’s not what limits are about: they’re about the trend in a function’s behavior near a value, and the trend near but not at h = 0 is definitely for 0/h to be 0. (Plugging the value being approached into the function is basically a special case that sometimes works, thanks to the limit laws, but it’s not the definition of limit.)

Graph with a flat line for 0 over h at y equals 0

The Chain Rule

Section 3.6

Warm-Up

What is the derivative of sin(3x)?

The chain rule applies because you have one function (3x) inside the argument to another (sin).

In sine of 3x, sine is the outer function and 3x the inner

Now plug the inner and outer functions into the chain rule formula:

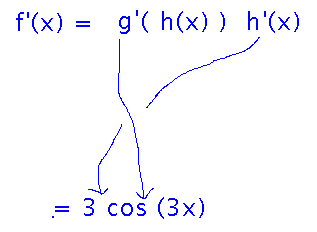
f prime equals g prime of h of x times h prime yields 3 times cosine 3x

Examples

Find dy/dx if y = cos( x⁵ + 2x )

This is similar to the warm-up example. The outer function is cos, and the inner is x⁵ + 2x.

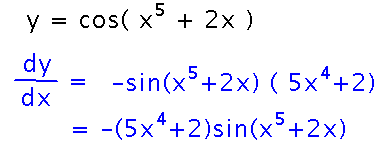
Using the chain rule on cosine of x to the 5th plus 2x

What about y = (x⁴ + 3x² - 6x + 9)⁵? Here the outer function is “raise to the 5th power,” and the inner is a long polynomial. Although the functions aren’t as clear as before, the chain rule formula still applies:

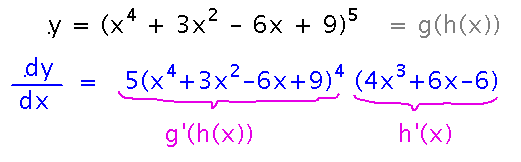
Using the chain rule on a long polynomial raised to a power

More practice with the chain rule.

Next Lecture