The Formal Definition of Limit, Part 2

Return to Course Outline

Previous Lecture

SI Session

This afternoon, 3:00 PM, in Bailey.

Questions?

Proving Limits

Example

... from last time.

Prove that lim_x→3 2x - 1 = 5

Strategy:

1. Give a way of finding δ from ε
2. Show that the δ you find really works, i.e., keeps 2x - 1 within ε of 5

For the first step, start with | f(x) - L | being less than ε, and see if you can get from there to something that looks like δ.

The for the second step, work from this δ forward until you confirm that |f(x) - L| is less than ε.

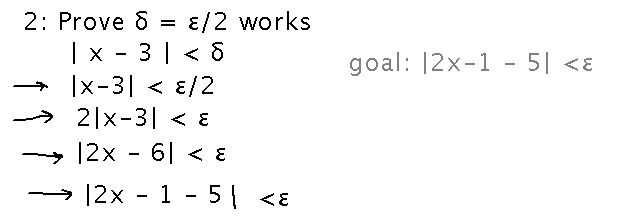
In this proof, the second step was basically the first one done backwards. Does this always happen? No, it’s mostly a consequence of the function in question being linear (i.e., its graph is a straight line). The book has an example of a limit of x² as x approaches 2 where the derivation of δ is more intuitive, and its result is that δ is the smallest of 2 possibilities. As a result, showing that x values within this δ of 2 produce y values within ε of 4 still involves ideas from the derivation of δ, but in ways that feel less like just doing that derivation in reverse.

Another Proof

Prove the limit law lim_x→a c = c where a and c are any constants.

Someone did essentially this in the limit game, with lim_x→1 3. The key realization was that no matter what tolerance you’re offered, 3 is always 3, it never varies. In a little more general form...

This sort of use is the real value of the formal definition. It’s too awkward to use to find specific limits, but it justifies the rules that make those specific limits easy to find.

Key Point

Limit laws (and other methods for reasoning about limits) all have reasons.

Next

Remember our discussion of calculating instantaneous speed from distance traveled.

Now that you know about limits, how would they help you solve this problem exactly?

Read section 3.1 about derivatives.

Next Lecture