The Formal Definition of Limit, Part 1

Return to Course Outline

Previous Lecture

Questions?

The Formal Definition of Limit

Section 2.5

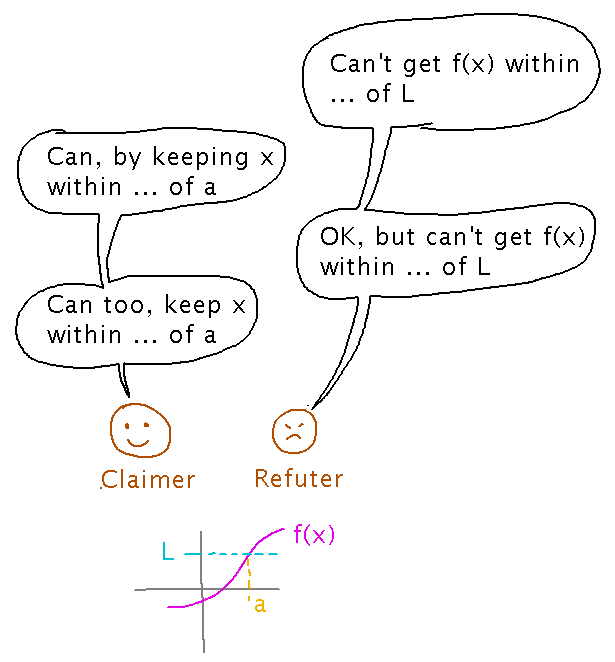
Limits as a Game

“Claimers” who claim that a certain limit equals a certain number, vs “Refuters” who try to show that it isn’t.

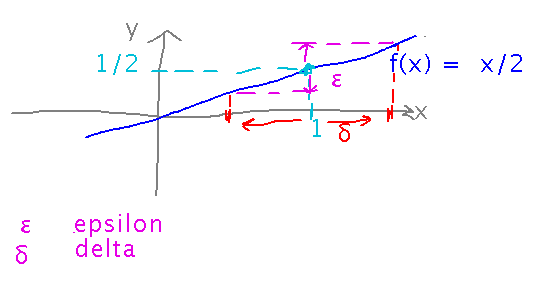
For example, consider the claim “lim_x→1 x/2 = 1/2”. A refuter might start by saying “I don’t think you can get x/2 to be within 1/4 unit of 1/2.” But then a claimer can rebut that by pointing out that if x is within 1/2 unit of 1, x/2 will be between 1/4 and 3/4, i.e., within a quarter of a unit of 1/2. The claimer might further support this claim with a graph of f(x) = x/2 to show that for every x between 1/2 and 3/2, f(x) is between 1/4 and 3/4.

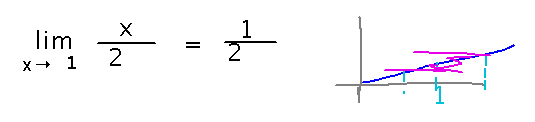
Try playing for a while...

What does this have to do with the reading? It’s getting at ε and δ: refuters need to suggest ε values, and claimers need to show that no matter what ε the refuters offer (since the definition of limit requires there to be a δ for all ε), they can find a δ that keeps f(x) within ε of the claimed limit.

A Proof

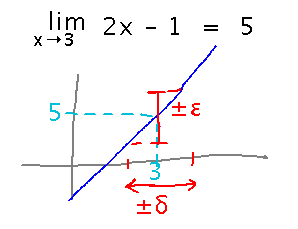
Show that lim_x→3 2x - 1 = 5

To do this we need to give a way (formula, method, etc.) to find δ for any given ε, and then show that that δ “works,” i.e., it keeps f(x) within ε of the limit. Coming up with that way to find δ was basically what claimers needed to do to win the limit game; finding an ε that it wouldn’t work for was what refuters needed to do to win.

Next

Finish this example limit proof.

Next Lecture