SUNY Geneseo Department of Mathematics
Friday, February 8
Math 221 03
Spring 2019
Prof. Doug Baldwin
SI session today, 3:00 - 4:30, Bailey 209.
Write down (probably as a piecewise definition) a function on [0,5] that has some discontinuities. Be able to say how each discontinuity fails the requirements for a function to be continuous at a point.
(Then we’ll combine some of the examples into a “master example” of discontinuity.)
To get started, think of some specific ways a function could be discontinuous. For example...
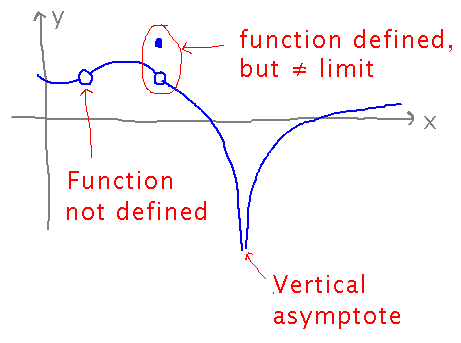
Try to come up with function(s) that exhibit some of these. For example...
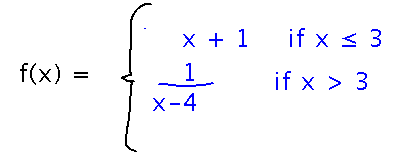
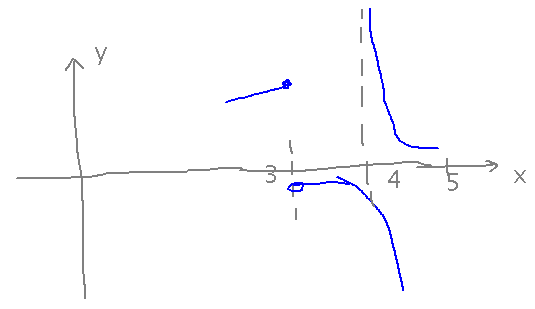
which should have a graph that looks sort of like this:
Formally, the requirements for a function to be continuous at a point are that...
In our example, the discontinuity at x = 3 violates the third requirement, while the discontinuity at x = 4 (the asymptote) violates the first two (and so the third can’t even come into consideration).
See more exactly what our discontinuous function looks like by plotting it with Mathematica.
Use Mathematica’s Piecewise function to define the function, then graph as normal.
Background: according to Einstein’s theory of relativity, the mass of a moving object depends on its speed; in the limit as speed approaches the speed of light, this mass becomes infinite. One consequence is that it would take an infinite amount of energy to make an object of non-zero mass travel at the speed of light.
Question: every good science fiction movie has space ships that travel faster than the speed of light. Suppose one of these spaceships accelerates from standing still to moving faster than light over a period of a couple of seconds. Is its speed a continuous function of time? (Assume that even in science fiction movies, spaceships have non-zero mass and there isn’t an infinite amount of energy.)
Answer: Speed can’t be a continuous function of time, because if it were there would have to be a time when the spaceship was traveling at the speed of light, requiring infinite energy:
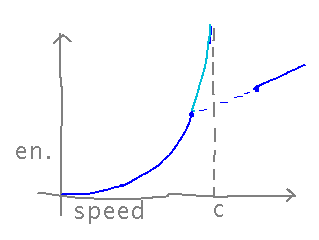
Formally, the idea that if a function (e.g., speed) is continuous between a and b, it has to take on every value between f(a) and f(b) is the Intermediate Value Theorem. Thus the mathematical reason science fiction spaceships must accelerate discontinuously from below the speed of light to above it is that if they didn’t then they would at some time have to travel at the speed of light by the Intermediate Value Theorem, but that’s impossible.
If everything in math has a reason, what’s really the reason for the limit laws, ability to algebraically simplify limits, etc?
We’ll look at the formal definition of “limit” from which those things follow.
Read section 2.5 in the textbook.