SUNY Geneseo Department of Mathematics

Infinite Limits

Thursday, February 7

Math 221 03
Spring 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Infinite Limits

Part of section 2.2

Example 1

What can you say about lim_x→1^- 1 / (x-1), lim_x→1⁺ 1 / (x-1), and lim_x→1 1 / (x-1)?

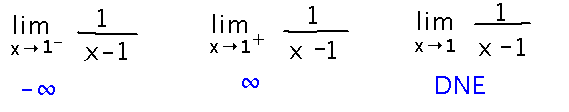
Limit from left is negative infinity, limit from right is positive infinity, so 2-sided limit doesn't exist

We built up quite a bit of intuition for why these are the right answers, for example by looking at plots such this one from Mathematica:

Two curves, one from left curves down towards minus infinity, one from right curves up towards positive infinity

For a more formal and rigorous reason to believe these limits, we can use the book’s infinite limits theorem about fractions of the form 1 / (x-a)ⁿ. Or, conversely, our experience with this example can provide intuition for why that theorem makes sense.

Some thoughts on reading math texts:

Read the first time to get a sense of what the main results are.
Expect to read more than once!
Read the second time, maybe guided by a need to use one of those main results remembered from the first reading, to understand a specific point.
- Try to translate ideas expressed mathematically into your own words for your own understanding
- Try to figure out why the claims are plausible
- Try to understand why the book needs to say all the things it does — generally every word is there for a reason.

What are the numeric values of any of the above limits? This is a trick question: none of them have numeric values, infinity is not a number (despite often being used in contexts where it seems like it is).

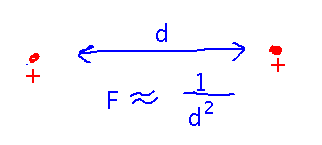
Do limits like this ever come up in practice? Yes: consider a physics problem in which you want to push 2 positively charged particles, say hydrogen nuclei, so close together that they merge into one particle. (This is a real thing. If you can do it in a reasonably controlled fashion it’s fusion energy, a long-promised but not-yet-realized green energy source; if you do it in a not-so-controlled fashion it’s a hydrogen bomb.) Because both particles are positively charged, they repel each other, and the strength of the repulsion is inversely proportional to the square of the distance between them. So energy scientists and weapons scientists and similar people are interested in how that force grows as the distance between the particles shrinks to 0, i.e., a limit that mathematically goes to infinity.

Positively charged particles separated by distance d, force is roughly 1/d^2

Limit Laws

What is lim_x→1 x / (x-1)²?

This isn’t in a form that the infinite limit theorem applies to, but you can use the product limit law to separate it into a limit you know how to evaluate, and one to which the theorem applies.

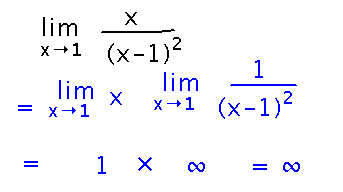
$Limit of fraction is product of limits of numerator and one over denominator$

Note that at the end here we made the reasonable assumption that 1 times an infinitely increasing value is also infinitely increasing, i.e., we treated infinity as if we could do arithmetic with it.

But Be Careful

Some attempts to do arithmetic on infinity go badly wrong. For example, here’s a wrong way to find lim_x→1 (x-1) / (x-1)². (And a correct way on the side.)

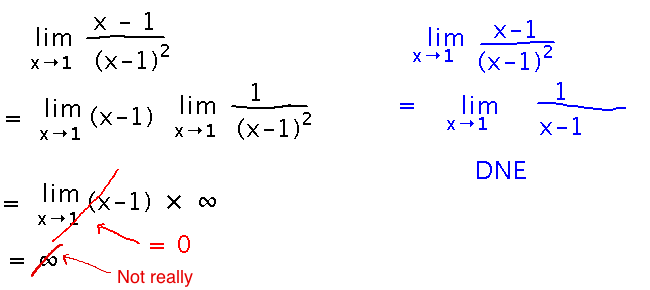
Product of terms where one goes to 0 and one to infinity gives misleading answers

Key Points

Theorem for recognizing infinite limits.

But be careful treating infinity as a number (it isn’t).

What does it mean to say a function is “continuous”?

Read section 2.4

Next Lecture