Geneseo Math 221 03 Algebra and Limits

Misc

SI Sessions

They start today (Feb. 1), from 3:00 - 4:30, in Bailey 209.

Continuing on, they’ll be every Wednesday and Friday from 3:00 - 4:30, Bailey 209.

Going is a really good way to get further exposure to and practice with the ideas we’re studying.

Problem Set 1 Dates

“Complete by” and “Grade by” dates for problem set 1 are now next Monday and Thursday, respectively.

See the announcement in Canvas for more information.

Questions?

Algebraically Simplifying Limits

“Additional Limit Evaluation Techniques” from section 2.3.

Trigonometry Review

(Since there are rich relationships between trig functions to take advantage of when they appear in limits.)

The short version: trigonometric functions relate angles to other quantities.

Some practical significance

Relating angles to distances
Since angles are periodic (turning past 360 degrees is the same as turning past 0), so are the trigonometric functions, which means they show up a lot in describing periodic physical phenomena, e.g., waves.

Definitions are in terms of the lengths of the sides of triangles.

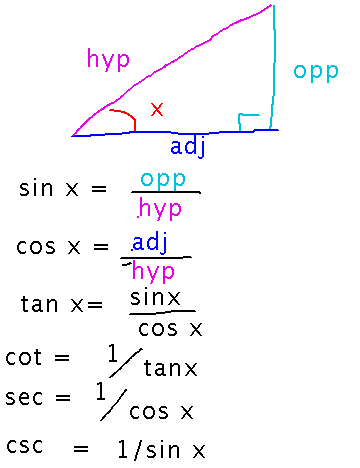
A triangle whose sides define sin and cos, which in turn define tan, cot, sec, csc

But these are not what you’re going to be working with most of the time — most of the time you’ll find yourself using identities or formulas derived from these definitions, not the definitions themselves. For example, the limit example later in this class.

Note on angle measures: mathematicians measure angles in radians, not degrees. So unless told otherwise, any angle measure in this course is in radians.

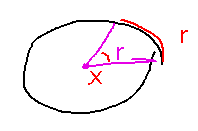
What is a radian? It’s the angle that subtends (i.e., encloses) an arc whose length is exactly the radius of the circle. Thus it’s no coincidence at all that there are 2π radians in a complete circle, and that complete circle’s circumference is also 2π times its radius.

A circle with an arc whose length equals to radius

Angle-to-Distance Example

If you drive 1 mile in a direction 30 degrees east of north, how far east have you moved? How far north?

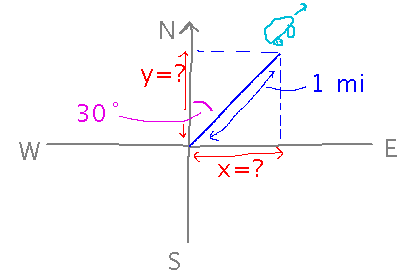
Car driving 1 mile at 30 degrees east of north

The key thing here is to realize that the distance you drove forms the hypotenuse of a right triangle whose legs are the easterly and northerly distances you want to find. Then you do use the definitions of trig functions, in particular that the easterly distance over the hypotenuse is the sine of your angle, and the northerly distance over the hypotenuse is the cosine:

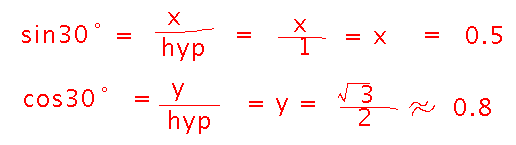
x = sin 30 degrees, y = cos 30 degrees

Identities

There are lots of trigonometric “identities,” i.e., formulas relating trig functions to each other.

For example, combining the calculations of easterly and northerly distance in the driving example with the Pythagorean Theorem suggests that sin²x + cos²x = 1. (This example generalizes even if the distance driven isn’t exactly 1 mile.)

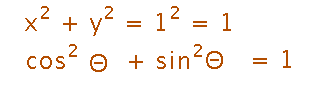
c^2 = a^2 + b^2 implies 1 = cos^2 + sin^2

See Appendix C.3 in our book for more, especially ones for doubled angles, halved angles, sums and differences of angles.

Limit Example

Find lim_x→0 2 sinx / sin(2x)

They key step here is finding the identity for sin(2x) and using it to simplify the expression in the limit:

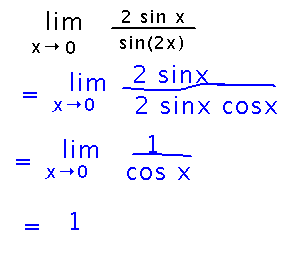
sin(2x) is 2 sinx cosx from which 2 sinx cancels, leaving limit equal to 1

More broadly, this is an example of the reading’s overarching point: simplifying limits you are trying to find often turns ones you can’t use limit laws on into ones you can.

Look at the “simplify” idea with algebra beyond just trig identities.

No new reading.