SUNY Geneseo Department of Mathematics

More about Algebra and Limits

Monday, February 4

Math 221 03
Spring 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Next SI session is Wednesday.

Questions?

How do you know where the function in problem set question 2 is undefined?

Look at the function’s definition, and ask yourself how it could be undefined. Dividing by 0 when t = 0 is the only way:

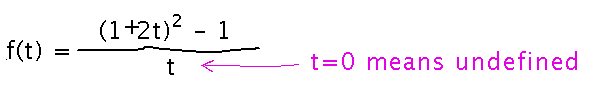
((1+2t)^2 - 1)/t, t = 0 means expression undefined

Conversely, for part B, any t value other than 0 makes f(t) defined. For example f(1) = 8. And at all such values all the limit laws apply, so the limit of f(t) is also defined, and can be calculated by simply plugging the t value into the formula for f.

Simplifying Limit Expressions

A series of examples of classic algebra moves for simplifying limits.

Factoring

Find lim_x→3 (x-3) / (x² - 9)

Plugging x = 3 into the expression in the limit gives 0/0. But the denominator is a difference of squares, which can be factored, leading to an expression that can be evaluated by the laws:

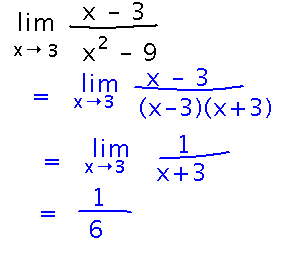
Factoring x^2 - 9 in denominator into x-3 and x+3 allows x-3 to cancel

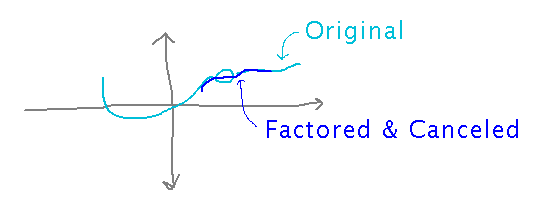
Why does this (and other simplifications) work? I claimed a week or so ago that factoring and canceling in particular produces a different function from the original, since the expression resulting from cancellation is defined at an x value where the original function isn’t defined.

But that new function is equal to the original everywhere except at the point where the original isn’t defined, and so must have the same limit as x approaches that point:

Graph of original and simplified functions follow same line, but original has a hole

Multiply by a Conjugate

Find lim_x→2 ( √(x-1) - 1 ) / ( x - 2 )

It would be really nice to get rid of the square root in the numerator (just to make the whole limit easier to work with). One way to do that is multiply numerator and denominator by its “conjugate” — the same 2 terms, but with the opposite sign between them:

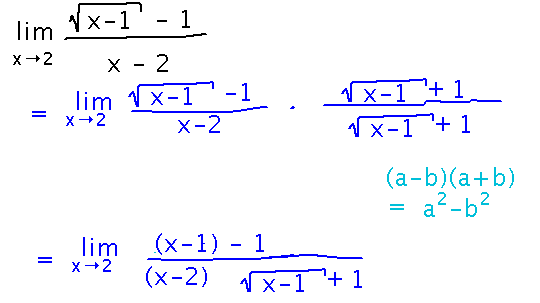
Multiply numerator and denominator by sqrt(x-1) + 1

Once you do this, the numerator conveniently simplifies to x-2 and cancels with part of the denominator, leaving you with a limit you can evaluate by the limit laws:

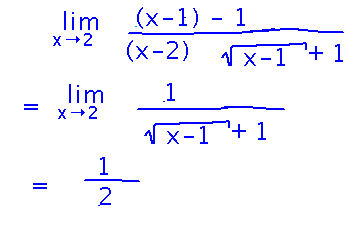
Limit as x goes to 2 of 1 / (sqrt(x-1)+1) = 1/2

Simplifying Fractions

Find lim_t→0 ( 3 / (1+t)² - 3 / (1+t) ) / t

The first thing to do with this is make the fractions simpler.

One way to do that is to factor the common multiple 3/(1+t) out of the numerator:

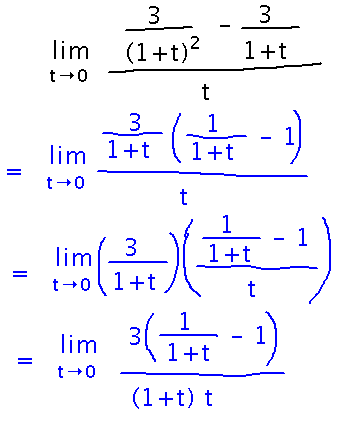
Factor 3/(1+t) out of numerator, then multiply (1+t) into original denominator

Now put what’s left in the numerator over a common denominator:

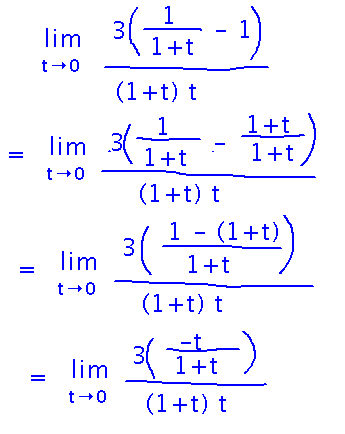
1/(1+t) - 1 becomes -t/(1+t)

Now there’s a -t in the numerator that cancels with t in the denominator:

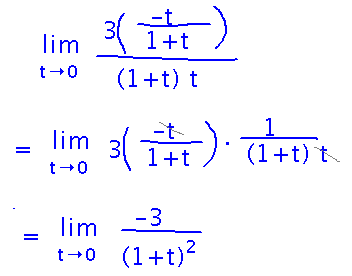
Cancelling -t in numerator and t in denominator leaves -3/(1+t)^2

And finally you can apply limit laws without anything being undefined:

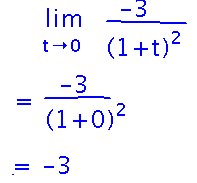
Limit as t goes to 0 of -3/(1+t)^2 is -3

It’s probably a little simpler to start by getting a common denominator for the terms in the numerator. This was one of two ways to approach this problem we mentioned in class, but I chose the one above to see how it would work. Here’s the other way done out:

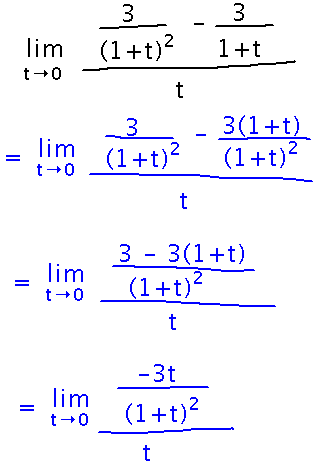
3/(1+t)^2 - 3/(1+t) becomes -3t/(1+t)^2

Now combine the denominators:

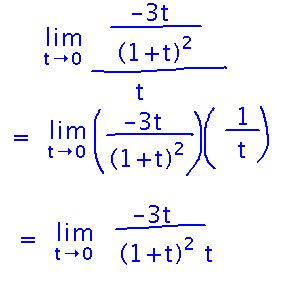
-3t/(1+t)^2 times 1/t becomes -3t / t(1+t)^2

And finally you can cancel t’s and apply limit laws:

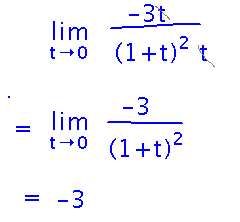
Limit as t goes to 0 of -3t / t(1+t)^2 is -3

We now have a pretty good set of tools for working with limits. Let’s go back and apply them to some variations on the limit idea.

Read the “One-Sided Limits” subsection of section 2.2 in the textbook and see how it approaches the problem.

Next Lecture