Limit Laws

Return to Course Outline

Previous Lecture

Misc

SI Sessions

They start this Friday (Feb. 1), from 3:00 - 4:30, in Bailey 209.

I encourage everyone to attend as a way to get further exposure to and practice with the ideas we’re studying.

Google Calendar

Demonstrate how to make an appointment.

Also see this tutorial from CIT:

Questions?

Mathematica

The core idea is the “notebook,” a place you can type commands and see results.

Here is an example notebook that contains today’s demonstration. You can download it to your own computer, and then open it in Mathematica to see the commands and results, try changing them or experimenting with variations or new ones, etc.

Basic operators: +, -, * (multiplication), /, ^ (exponentation)

Functions: for example, Sqrt, Sin, etc. Arguments go in square brackets.

Plotting simple functions: the Plot function.

You can find documentation on Mathematica online at https://reference.wolfram.com/language/

Limit Laws

Beginning of section 2.3.

Example 1

Find lim_x→0( x² - 2√(x+1) )

The short version is that you can plug x = 0 into x² - 2√(x+1). The justification for why you can do this is the limit laws and the fact that they apply because all the necessary inner limits exist.

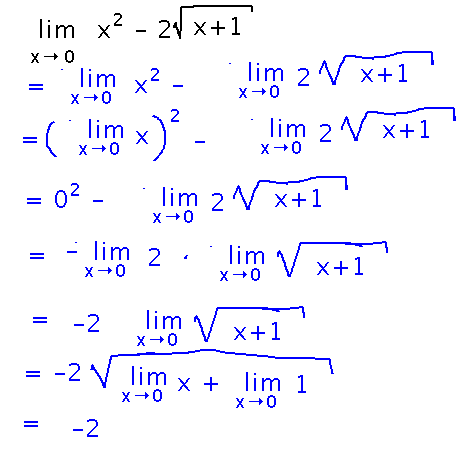
Key Points

Most of the limit laws (except for the ones that say lim_x→ax = a and lim_x→ac = c) can all be remembered as one overarching rule: you can move limits inside other operators (addition, subtraction, multiplication, division, exponentiation) as long as the inner limits you thus encounter are defined (and, in the case of division, the limit of the denominator isn’t 0).

So you can often take a limit by plugging a value for x into the function in question.

But beware that “often” is a vague word that implies you can’t always do this. So we need ways to tell when you can’t, and what you can do instead. Which brings up...

...Next

Can you use limit laws to find lim_x→0( x / (x²- 2x) )? No, because if you plug x = 0 into x / (x²- 2x) you get 0/0, and violate the quotient law’s requirement that denominators not be 0.

Look at some more powerful techniques to use with the limit laws to find limits.

Read the “Additional Limit Evaluation Techniques” subsection of section 2.3. But stop after example 2.20 (the remaining examples apply the laws and techniques to variations on limits that we haven’t talked about yet).

Next Lecture