Misc
SI
This afternoon: 3:00 - 4:30, Fraser 104.
Study Day Review Session?
Would you like an hour or so of review with me on Study Day (Tuesday December 10)?
Yes.
Questions?
Problem Set Question 1
(Integrals and areas related to a graph consisting of semicircular and triangular pieces)
How to integrate the functions for the pieces of the graph?
Actually, you don’t need to do it symbolically — use the idea that integrals are (signed) areas, and the fact that the pieces of the graph are shapes with known area formulas instead.
The difference between “integral” and “area” in the 2 parts of the question reflects the fact that area below the x axis has to be treated as negative in an integral, but positive if viewed as area. The two parts don’t imply different techniques for calculating areas/integrals.
Problem Set Question 5
(Area between a sine curve and the x axis.)

Use definite integrals to find the area, but be careful to integrate the positive and negative parts of the curve separately, and use the absolute value of the integral of the negative part of the curve.
Also note that sin x crosses the x axis at x = π and 2π, even if it looks on the graph like 3 and 6.
Integration by Substitution
First part of section 5.5.
Process
…As we have seen it by the end of class.
To evaluate the indefinite integral of g(x) dx
- Identify a u such that g(x) dx can be written as f(u) du
- Integrate f in terms of u
- Rewrite u in terms of x
More Examples
Find the antiderivative of sin2x cosx
Pick u = sin x and du = cos x dx to fit into the “un du” pattern:

How about sinx cosx?
This allows either of 2 substitutions. Following what we did in the previous example, you could pick u = sin x, so that du = cos x dx, and proceed as we’ve done before:
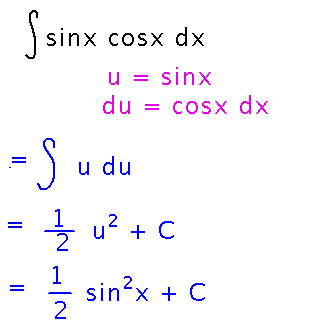
But you could also pick u = cos x and du = -sin x dx. This looks wrong at first, because it requires a negative sine and the integrand has a positive one, but that’s fixable: look a little deeper at the statement du = -sin x dx, and realize that it implies -du / sin x = dx, i.e., you can think of substitution as replacing dx with an expression involving du in which everything except the du eventually (hopefully) cancels out with other parts of the integrand, leaving you with an integration that only involves u:
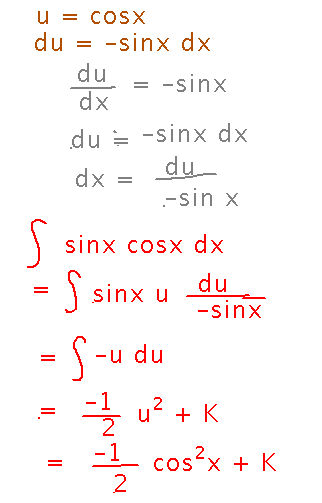
Morals: First, there are sometimes multiple substitutions you can use to evaluate an integral. Second, substitution can include multiplying integrands by constants to make u and du “line up” exactly with the integrand. This makes substitution a much more flexible technique than it might seem at first.
Did these two integrations just get different answers for the same problem? Not really, thanks to the identity sin2 + cos2 = 1 and the ability of constants of integration to be any constant:
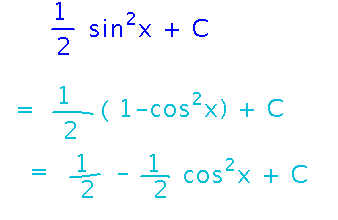
An example that came up recently in my computer graphics course: the antiderivative of cos (πx/2W) where W is a constant.
Use the substitution u = πx/2W. Moral: substitutions can be for any “inner function” in an integrand, they don’t have to be parts that are raised to some power (like our examples so far have been).
Also notice that this substitution also involves multiplying the original integrand by a constant to get u and du to match that integrand.
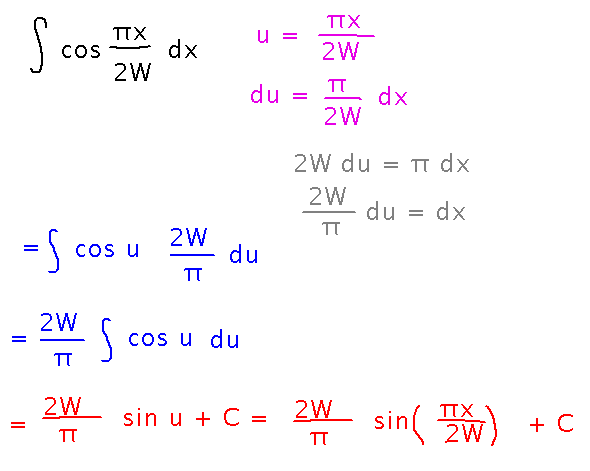
Next
Some more examples of fairly sophisticated substitutions.