Geneseo Math 221 06 Properties of Integrals

Misc

SI today! 3:00 - 4:30, Fraser 104.

Questions?

Key Idea(s)

There are algebraic rules for simplifying integrals: sum & difference rules, constant multiple rule; and you can split a long interval into contiguous parts and evaluate an integral over the long interval as a sum of integrals over the parts.

Integrals can be negative as well as positive.

…So beware when using integrals for area and f(x) might be negative.

Mathematica can compute integrals, via the Integrate function

Properties of Integrals

(Particularly ones that help you avoid Riemann sums)

Area Formulas

Last time we saw that the integral from 0 to 3 of x is 4 1/2.

Is there a way to confirm this via area formulas from geometry?

Yes, realize that the area under the line y = x is a triangle, and use the triangle area formula:

Integral of x is the area of a triangle, and can be computed as half the width times the height

Algebraic Properties

We have also figured out that the integral from 0 to 3 of x² is 9.

What about the integral of 3x² -x from 0 to 3? Use Example 5.11 as a guide to getting started, but continue past it by plugging in actual numbers for the integrals it leaves you with.

Use the difference and constant multiple rules:

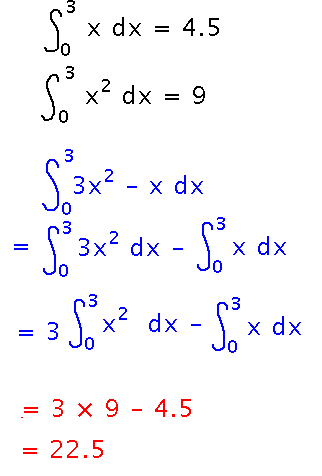
Split a large integral with the constant multiple and difference rules and evaluate the parts

Signed Area

What is the integral of x from -1 to 0?

It’s negative, which is unintuitive if you’ve been thinking of an integral as an area (areas are always positive). But it makes perfect sense in terms of a Riemann sum, because the f(x_i) terms in such a sum will be negative wherever f is negative.

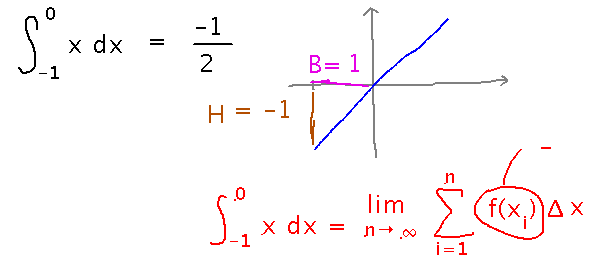
The integral of a negative function is also negative

Moral: The Riemann sum is the official definition of “integral.” Where it and intuitive understandings (e.g., integral is area) conflict, the definition wins.

What about integrating x from -1 to 3? Asking for this as an integral leads to a different answer than asking for it as an area does, because of the possibility that integrals can be negative.

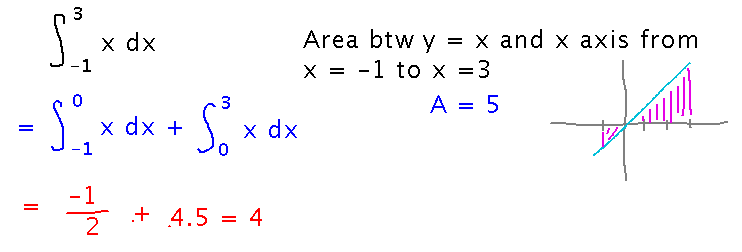
Integral of positive and negative function is sum of signed parts; area is sum of absolute values

Integrals in Mathematica

The Integrate function computes them.

See this notebook for an example.

The Fundamental Theorem of Calculus.

Read “The Mean Value Theorem for Integrals” and “Fundamental Theorem of Calculus Part 1: Integrals and Antiderivatives” in section 5.3.