Riemann Sums

Return to Course Outline

Previous Lecture

Questions?

Riemann Sums?

Question 5 on problem set 11.

The first part of the question wants you to estimate an integral via a Riemann sum with 100 intervals. Start by drawing diagrams and writing down facts in order to start to see how things fit together.

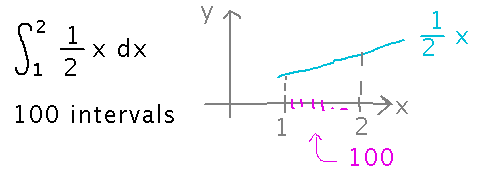
Now lay out the general form of a Riemann sum, and try to fill in the pieces based on the picture and givens.

Finally, plug the pieces into the general form to get the specific Riemann sum.

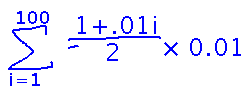
From here you can finish the question by using algebra and closed-form rules for summations to simplify and evaluate.

Sums in Mathematica?

Can Mathematica do sums?

Yes it can.

Use the Sum function, which has 2 arguments: the expression to sum, and the summation variable and its bounds.

This notebook has examples of Sum used to evaluate summations both numerically and symbolically.

Practice Riemann Sums

What is the integral from 0 to 3 of x, as a limit of a Riemann sum?

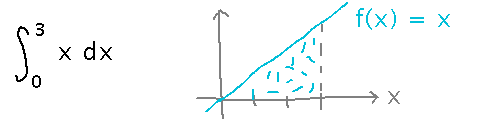
The exact value of the integral is the Riemann sum’s limit as the number of intervals approaches infinity.

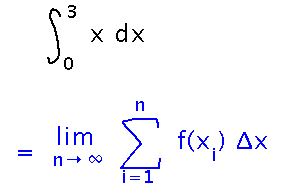
Identify delta x, and the x-sub-i (which also give you the function values, since f(x) = x).

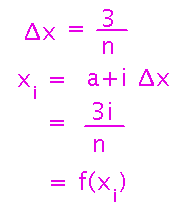
Plug what we just found into the limit / Riemann sum, and use summation rules to simplify.

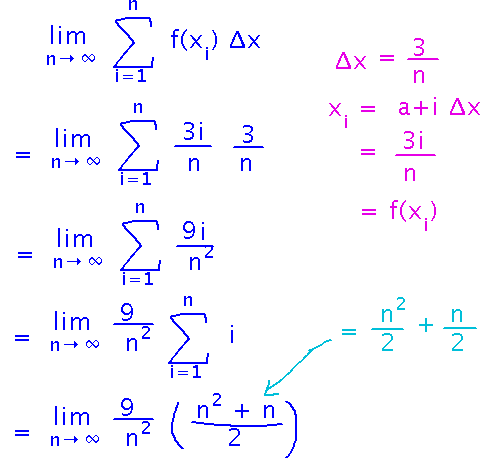
Finally, limit laws for limits at infinity give you the exact answer:

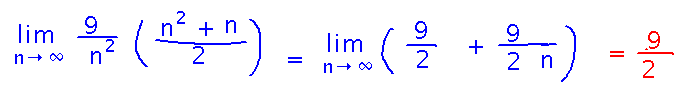
Next

Pick up here and compare this result to what geometric arguments suggest, then look at other ways to avoid evaluating Riemann sums.

Next Lecture