Misc
Course Advising for Math Minors
Today, 2:30, South 328.
(And similar advising for math majors today at 2:30 in South 332)
Print Copy of Textbook
If anyone would like a paper copy of our textbook, you can now order one from Barnes and Noble.
Go to the store and let the assistant manager, Bill McCarthy, know you want a copy of the OER textbook for Math 221.
Cost is $65.00.
GROW STEM
College organization supporting women and minority students in STEM.
Meeting today (and every Wednesday, I think), 7:00 PM, Newton 209.
Discussing recent all-women spacewalk.
Questions?
The Mean Value Theorem
Section 4.4.
Key Idea(s)
Rolle’s Theorem: If a differentiable function has the same value at the ends of some interval, then it has a derivative of 0 somewhere in that interval:
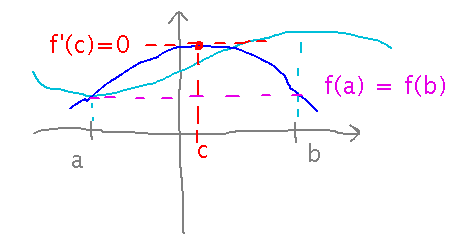
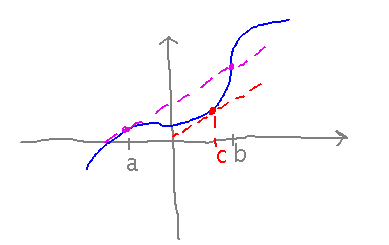
Mean Value Theorem: A function that is differentiable over some interval has a derivative somewhere in that interval that is equal to the slope of the secant line between the endpoints of the interval:
Example
Let f(x) = 5x - x2; where between x = 1 and x = 3 is the “c” promised by the Mean Value Theorem?
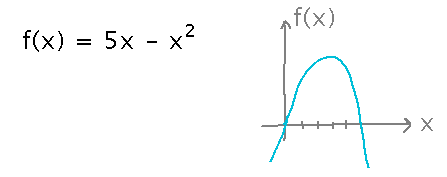
Start by finding the slope of the secant line between points (1,f(1)) and (3,f(3)).
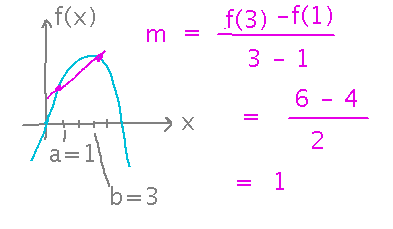
Then find the derivative of f, and solve for the value of x that makes the derivative equal the slope. That value is c.
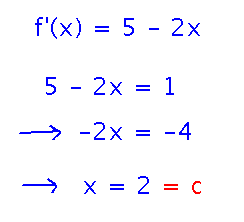
Application Example
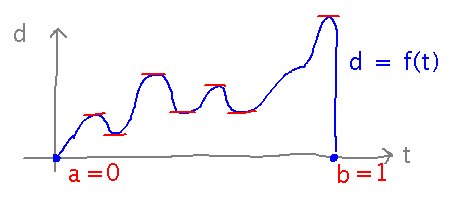
Geneseo’s college flying carpet flies from Geneseo to Rochester and back, taking 1 hour to make the trip. Function f(t), 0 ≤ t ≤ 1, gives the distance between the carpet and Geneseo during the flight, and f’(t) gives the carpet’s speed relative to Geneseo — positive speed means the carpet is receding from Geneseo, negative that it is approaching. Assuming that even a magic flying carpet has a continuous and differentiable distance function f(t), was the carpet’s speed ever 0 at any point other than t = 0 and t = 1 during the trip? How do know?
Yes, it must be by Rolle’s Theorem (or the Mean Value Theorem): distance is 0 at both endpoints of the trip, and so by Rolle’s theorem there must be a point where the derivative of distance, i.e., speed, is 0. Equivalently, the slope of the secant line between the endpoints is 0, so by the Mean Value Theorem there must be some point with a derivative of 0.
A Theoretical Consequence
Do the antiderivative formulas we have really give all the antiderivatives of their functions? Couldn’t a devil’s advocate argue that there are weird functions we haven’t necessarily seen yet that have the same derivatives as simpler ones?
For example, even though we know that antiderivatives of products aren’t just products of antiderivatives (or at least we suspect it since the analogous claim holds for derivatives), doesn’t something like this suggest that f(x) = x might have an antiderivative that is some weird combination of polynomials and logarithms?
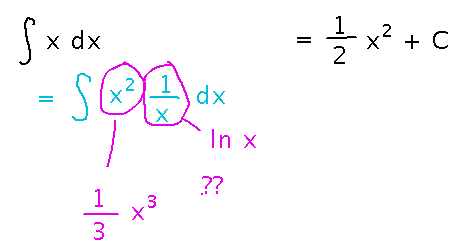
Why or why not?
The devil’s advocate is wrong. One of the consequences of the Mean Value Theorem says that if 2 functions have the same derivative then they can only differ by a constant.
Next
Derivatives and the shapes of graphs.
Read section 4.5.