SUNY Geneseo Department of Mathematics

Absolute Extreme Values

Monday, October 21

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

PRISM Peer Advising

Wednesday, October 23, 2:30 PM, South 332.

SI Today

6:00 - 7:30, Fraser 104.

Questions?

Equation for tangent line? The basic situation is that you know a point on the graph of some function, namely the point at which you want the tangent. You can also figure out the slope of the tangent by finding the derivative of the function. Then use either the point-slope equation for a line, or the tangent line equation used for linear approximation (which are closely related to each other):

Tangent has slope f prime of a and equation y minus f of a equals f prime of

Absolute Extrema

“Locating Absolute Extrema” in section 4.3.

Key Idea(s)

Definitions: absolute minimum is the smallest value the function attains; absolute maximum is largest. May be over entire domain, or some interval within it.

Absolute extrema might occur at critical points, but there can be critical points that correspond to local but not absolute extrema, and…

…If you are looking for absolute extrema over a closed interval, they might be at the endpoints.

Procedure for finding absolute extrema:

  1. Find critical points
  2. Evaluate function at critical points
  3. If working with a closed interval…
    1. Evaluate function at endpoints
  4. Absolute minimum is the smallest of all the values you found, absolute maximum is largest.

Example

Where (if anywhere) are the absolute minimum and maximum of f(x) = x2 + 4x + 4?

Start by finding critical points, i.e., places where f’(x) is 0:

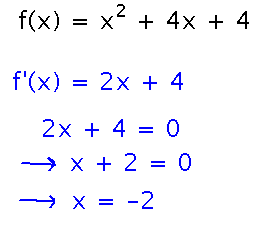
Finding critical point at x equals minus 2

This one critical point could be the absolute maximum or minimum (or could be neither, not all critical points are maxima or minima). Any absolute extrema not accounted for by this critical point don’t exist -- because on either side of the critical point the derivative is either positive (so f is increasing) or negative (so f is decreasing), and can’t change sign without going through 0 and creating another critical point (as long as the derivative is continuous, which this one is). Calculating derivatives at arbitrary points on either side of the critical point and looking at their signs thus tells us a lot about what if any sort of absolute extremum we have at the critical point:

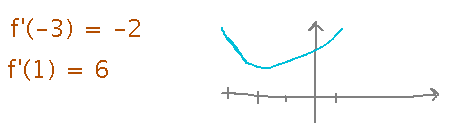
Signs of derivative around minus 2 show that absolute minimum happens there

Since the function goes from decreasing to increasing at the critical point, that point must correspond to a minimum, and the absolute one at that. As you move away from this point, the function’s value increases without bound, so there is no absolute maximum.

A More Realistic (?) Example

The Mount Doom ski slope has elevation h(s) where s is distance from the endpoint of the slope given by h(s) = (2/3) s3 - 3s2 + 4s, over the interval 0 ≤ s ≤ 3.

Line rising steeply from origin, turning briefly down and then rising again

Where are the highest and lowest elevations on the ski slope?

Start, as in the first example, by finding critical points:

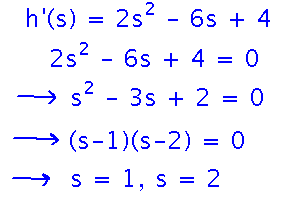
Derivative of height has critical points at 1 and 2

But now notice that the ski slope is defined over a closed interval, and the function’s values at the critical points aren’t as extreme as the values at the endpoints. This is an example where the absolute extremes over this interval are at the endpoints rather than at any critical points.

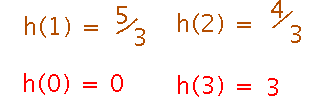
f of 0 is smaller than f at either critical point, f of 3 is bigger

Next

The Mean Value Theorem

Read section 4.4.

Next Lecture