Local Extreme Values

Return to Course Outline

Previous Lecture

Questions?

How to write “ln” in Mathematica? Use the Log function. See the first few lines in this notebook for examples.

Extreme Values

Section 4.3

(But particularly local extrema today.)

Key Idea(s)

A first derivative being 0 tells you where extrema might be, i.e., if f’(a) = 0 then f might have a maximum or minimum at x = a.

Example

Where are the local extrema of f(x) = 3x⁴ +4x³ - 12x² + 1?

Solving this, or other local extrema problems, involves 3 general steps:

First, find the derivative of f:

Second, solve for values of x that make the derivative 0. If the derivative is a polynomial (or sometimes even if it isn’t), factoring it can be a good way to find these values, since any value that makes one factor 0 makes the whole function 0:

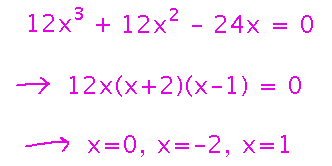
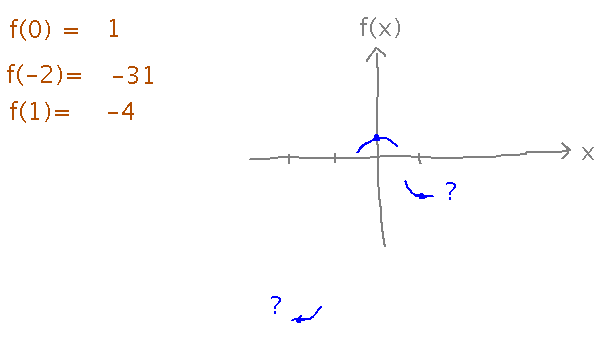
Finally, find the values of f(x) at each place where f’(x) = 0, and try to determine whether they are maximums of minimums. Later we’ll see analytical techniques that can help with this, but for now thinking about how the function must get from point to point, and plotting, can help.

Mathematica

Solving local extrema problems with Mathematica. Using a tool such as Mathematica is far easier than doing things like plotting, or evaluating a function at lots of points, or even solving complicated equations by hand.

Here is an example of how you could use Mathematica on the example above.

The key new feature is probably defining a function, analogous to saying “let f(x) = …” in math. In mathematica you write the function with square brackets around its argument, and an underscore after the argument name, and using := instead of “let ... =,” for example

 f[x_] := 3 x^4 + 4 x^3 - 12 x^2 + 1

Next

Absolute extrema.

Read (or re-read) the “Locating Absolute Extrema” subsection of section 4.3.

Next Lecture