Misc
Colloquium:
Dr. Robert Rogers, SUNY Fredonia
“Where Am I Ever Going to Use this Stuff?”
Today (October 16), 2:30 - 3:30 PM, Newton 201
Extra credit for going and writing a paragraph explaining connections you make to the talk.
Questions?
How to express π and various other functions in Mathematica? See some examples here.
More Related Rates Problems
Section 4.1 in the textbook.
Car and Pedestrian
From last time, how fast are a car and pedestrian closing on each other as they both approach a crosswalk?
Last time we described the problem and found the derivative of distance with respect to time:

Now work out the actual numeric value for the distances and speeds given.
This just requires plugging in values for w, c, and their derivatives:
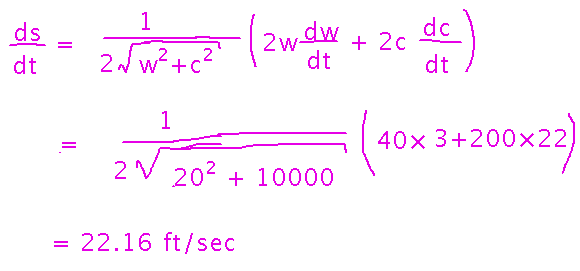
Pouring Pancakes
Suppose you’re cooking pancakes, pouring batter onto the griddle at a rate of 1 cubic inch per second. Considering a pancake to be a cylinder with constant height 0.1 inches, how fast is the radius of the pancake increasing when it is 2 inches?
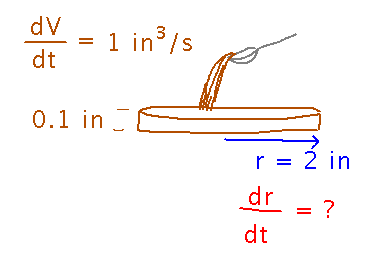
Find an equation that relates V and r, then take derivatives of both sides to get an equation that relates their derivatives. Use this equation to find dr/dt in terms of the other quantities:
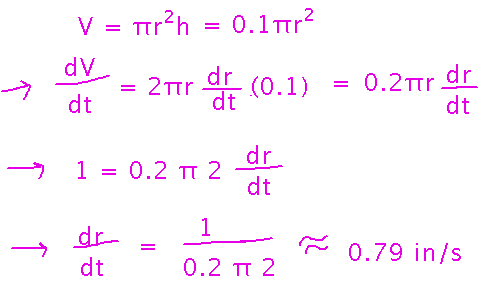
Hidden Spy
Jane Bond is trying to sneak into Dr. Evil’s secret lair. She’s hiding behind the wall of the lair while cameras mounted on telescoping poles search for intruders. Depending on how high the camera’s pole is, there is a safe region behind the wall in which the camera can’t see her. How fast is this region shrinking if the camera has height 5 meters and is rising at a rate of 1/2 m/s? The pole is 2 meters from the wall, which is 4 meters high.
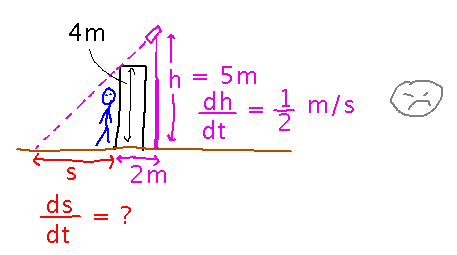
This is typical of related rates problems in which the key to relating the rates in question is similar triangles (i.e., triangles with the same angles). In particular, in a pair of similar triangles, the ratios between pairs of corresponding sides are all the same. In this case the triangle whose sides are the pole and the line from its base to the end of the safe region is similar to the triangle whose sides are the wall and the line from it to the end of the safe region (there are other pairs of similar triangles in the problem too, but this pair will do):

Extra credit opportunity: finish solving this problem and show me the result as part of grading problem set 6.
Next
Linear approximation.
Read section 4.2