SUNY Geneseo Department of Mathematics

Introduction to Related Rates Problems

Friday, October 11

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Colloquium next week:

Dr. Robert Rogers, SUNY Fredonia

“Where Am I Ever Going to Use this Stuff?”

Wednesday (October 16), 2:30 - 3:30 PM, Newton 201

Extra credit for going and writing a paragraph explaining connections you make to the talk.

Questions?

Related Rates Problems

Section 4.1

Key Idea(s)

These problems ask for a derivative of some quantity calculated from other quantities.

How to solve these problems

  1. Write down what you’re given, with a picture
  2. Express the quantity whose derivative you want in terms of the other quantities
  3. Take the derivative, typically using the chain rule
  4. Plug in numbers from the problem.

Silo

There’s an old silo in the field behind my house that casts a shadow across the field as the sun rises:

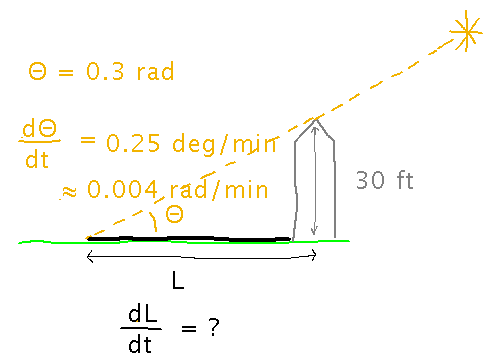
30 foot silo casting shadow of length L from sun at angle Theta

How fast does the shadow move across the ground when the sun is about 17 degrees (0.3 radians) above the horizon?

Start with “express the quantity whose derivative you want in terms of the other quantities.” In this case the key realization is that two of the numbers in the problem let you compute the tangent of the important angle:

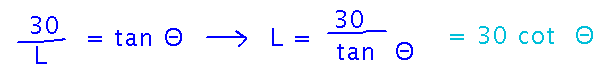
30 over L equals tangent of Theta so L equals 30 over tangent Theta

Now take derivatives with respect to t (which forces you to use the chain rule on any terms involving Θ), simplify, and finally plug in the numbers you know for Θ and dΘ/dt.

Derivative of L is minus 30 times secant squared Theta over tangent squared Theta times d Theta d t

Notice another advantage of Leibnitz notation in these problems: it makes the chain rule look very much like multiplication of fractions with cancellation, which can (1) be a good way to remember the chain rule in general, and (2) can help you see where and how to use it in related rates problems, e.g., if you find yourself calculating dy/dx and what you need is dy/dz, the Leibnitz form chain rule notation suggests multiplying by dx/dz.

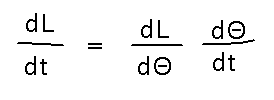
d L over d t equals d L over d Theta times d Theta over d t

Pedestrian and Car

(A “real world math bounty” problem from a past offering of this course.)

A pedestrian and a car are approaching a crosswalk at right angles to each other. How fast is the separation between them changing?

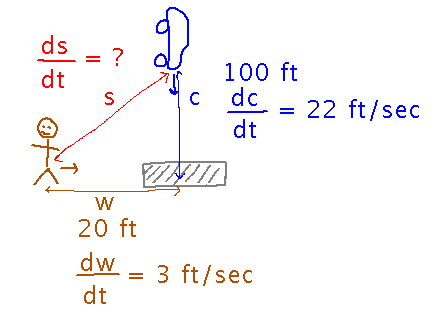
Car and pedestrian approaching crosswalk from perpendicular directions

Use the Pythagorean Theorem to relate w, c, and s.

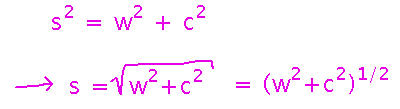
w squared plus c squared equals s squared, so s equals root w squared plus c squared

Now differentiate:

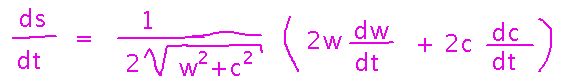
Calculate d s over d t via the power rule and multiple uses of chain rule

Next

More practice with related rates.

We’ll simplify the pedestrian-and-car result and plug in numbers.

We’ll also look at some more examples.

Next Lecture