The Chain Rule

Return to Course Outline

Previous Lecture

Misc

Friday’s Derivation and “Doing Math”

“Doing math” involves...

• Not knowing what the answer is ahead of time
• Not even knowing exactly how to get the answer
• … but knowing what methods might help and being willing to try them
• Revising answers

First Hour Exam

Next Monday, October 7, in class.

Covers material from problem sets 1 through 5 (i.e., the problem sets that will have been graded by the day of the exam).

You’ll have the whole class period.

Probably 3 to 5 short-answer questions, focusing on applying ideas from the course.

I’ll make some sample questions available.

Open book, open notes, open computer as a reference/calculator; closed person.

SI Session(s)

Today, 6:00 - 7:30, Fraser 104.

3-hour session Thursday.

Questions?

The Chain Rule

Section 3.6.

Key Idea(s)

The chain rule applies when an outer function is applied to an inner one, for example f(u(x)).

The basic rule says you multiply the derivative of the inside function by the derivative of the outside one (applied to the inside function).

For example, f(u(x)) differentiates as f’(u(x)) u’(x).

Examples

Find the derivative of f(x) = (x² - 6x)³.

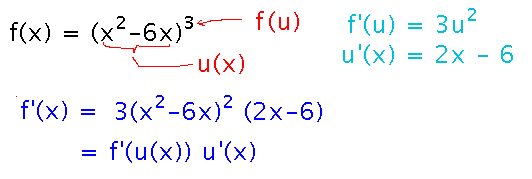
How about the derivative of sin(3t² + 1)

How about of sin( 180 t / π )?

(This is interesting because 180 t / π is how you convert t radians to degrees — this example illustrates that derivatives of trigonometric functions are different depending on whether you measure in degrees or radians.)

Next

The exponential function and its derivative.

Read “Derivative of the Exponential Function” in section 3.9.

Next Lecture