Questions?
Proving Difference Rule?
For the question in problem set 4 that asks you to prove the difference rule, I’m envisioning answers that start with a function that is the difference of two others, and the limit definition of derivative, and that end with the difference rule:
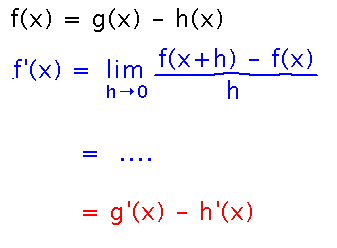
Mathematica?
Mathematica may give different answers from what you get when calculating derivatives, but those answers should be simplifiable to yours, either by Mathematica or by hand. For example...
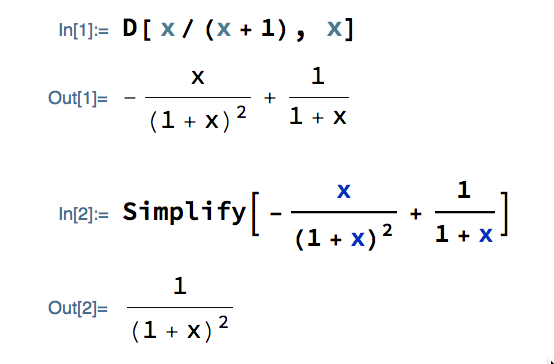
Trigonometric Derivatives
As an example of trigonometric differentiation rules, try finding the derivative of 2 cos x - cot x sec x.
There are at least 2 ways to go about this. One rewrites cotangent and cosecant in terms of sine and cosine and then differentiates:
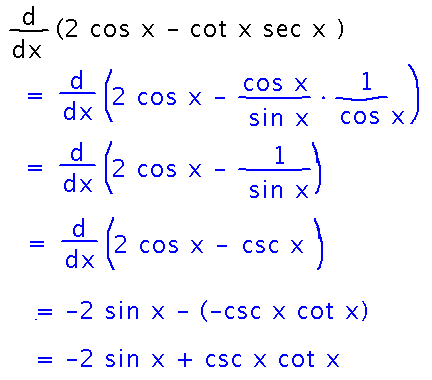
The other uses the product rule to differentiate the “cot x sec x” term and then simplifies. (This uses slightly different trig identities than we used in class in order to give a shorter derivation, but is similar in exercising a number of trig definitions and algebra techniques.)

Key points from both solutions are using trigonometric differentiation rules, and how those rules combine with previous rules for sums, differences, products, etc.
Trigonometric Antiderivatives
Key antiderivative rules that follow from the differentiation rules we’ve found:
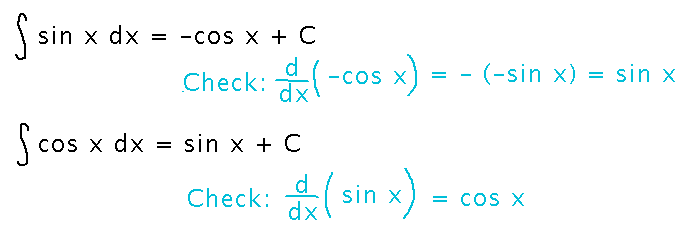
As you see more antidifferentiation rules, it’s helpful to know that they are collected in tables at the end of nearly every calculus book (including ours). You need to remember where to look them up more than remember what all the rules are.
The same is true of differentiation rules.
Next
The chain rule.
Read section 3.6.