SUNY Geneseo Department of Mathematics

Derivatives of Trigonometric Functions

Thursday, September 26

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

SI session this afternoon 3:00 - 4:30, Fraser 104.

Questions?

Derivative of Sine (and Cosine)

Section 3.5

Key idea: proof via the limit definition of derivative, with some apt uses of the squeeze theorem to find certain crucial limits.

Use these ideas to show that the derivative of cos x is -sin x.

Start with the limit definition applied to cosine:

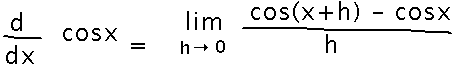
Derivative of cosine is limit as h goes to 0 of cosine x plus h minus cosine x all over h

Then use a trigonometric identity to expand cos(x+h):

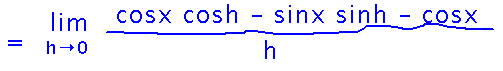
Cosine x plus h is cosine x times cosine h plus sine x times sine h

Then rearrange to separate terms involving x and terms involving h (rationale: any terms that involve x are just constants as far as limits as h approaches 0 are concerned, and so will be easy to evaluate; remaining terms involving h will hopefully be evaluable via limit laws or similar).

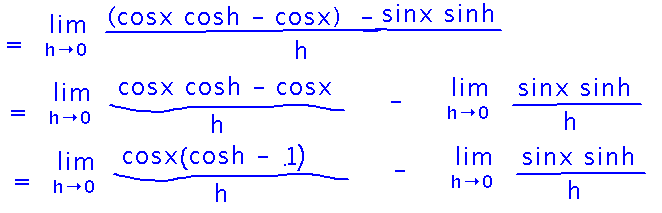
Limit becomes limit of product of cosines minus limit of product of sines

Finally, the limits with h in them can be evaluated via the squeeze theorem. One goes to 0 and the other to 1, leaving a simple expression for the derivative.

Limit of cosine h minus 1 all over h is 0, limit of sin h over h is 1

Derivatives of Other Trig Functions

Show that the derivative of sec x is sec x tan x.

Key idea: proof via the quotient rule, which is the crux of all derivations for trig functions besides sine and cosine.

secx = 1 / cosx

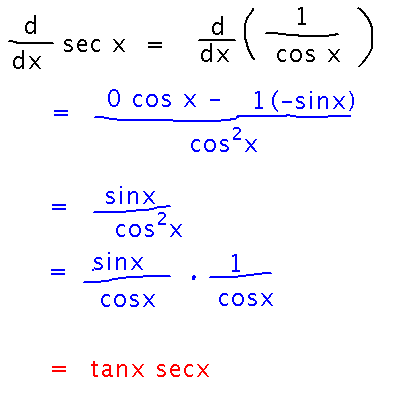
Apply quotient rule to 1 over cosine x to get sine x over cosine x times 1 over cosine x

Next

Key trigonometric antiderivatives, maybe examples of applying trigonometric differentiation rules.

Then the chain rule.

Read section 3.6 of the textbook.

Next Lecture