SUNY Geneseo Department of Mathematics

The Squeeze Theorem

Wednesday, September 25

Math 221 06
Fall 2019
Prof. Doug Baldwin

Questions?

Agenda

Find derivatives of the trigonometric functions.

To do that we need to go back to the limit definition of derivative, which implies finding limits of trig functions, which we don’t formally have ways to do.

So we start with a new theorem about limits that is particularly helpful with trig functions.

The Squeeze Theorem

Subsection “The Squeeze Theorem” in section 2.3.

Key Idea(s)

If h(x) ≤ f(x) ≤ g(x) around a and the limit of g = the limit of h, then the limit of f also equals that limit.

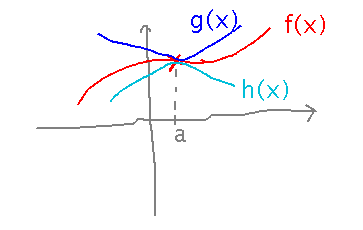
Graph of f pinched between graphs of g and h

Example

Textbook check exercise 2.19.

What is lim_x→0 x² sin(1/x)?

Notice that the sine of anything is always between -1 and 1, so multiplying x² by sin(1/x) gives you a product between -x² and x². That realization sets you up to use the squeeze theorem:

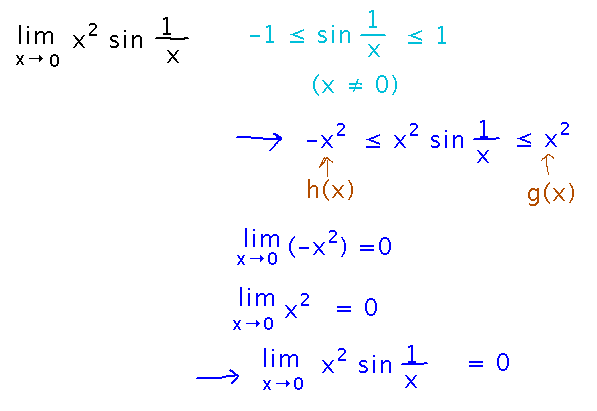
x squared and minus x squared both go to 0 as x goes to 0, and so squeeze x squared times sine 1 over x to 0 too

Limits of Sine and Cosine

Classic clever proofs, mostly all in the textbook, but good examples of reading math supplemented with diagrams (the proof about the limit of sinx as x approaches 0) and how several individually small results eventually combine to give you something important (the limit of sine, or cosine, as x approaches a specific value, combined with a seemingly obscure theorem about continuity of compositions of functions, gives a general rule for all limits of sine or cosine).

lim_x→0 sinx = 0: based on “squeezing” sinx between 0 and x. See the textbook’s Figure 2.29.

lim_x→a sinx = sina: proven in the course of proving that sin is continuous everywhere; Theorem 2.10 (which actually shows the proof for cosine, but sine is similar).

Derivative of Sine

Can we work out what the derivative of sinx is?

None of our derivative rules (power rule, product rule, etc.) apply here, but we can always fall back on the limit definition of the derivative:

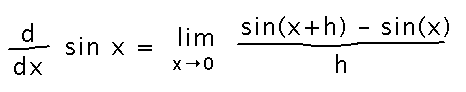
Derivative of sine x is the limit of sine of x plus h minus sine of x all over h, as h goes to 0

This doesn’t immediately give us a derivative, but there’s a plausible next step, namely check for a trigonometric identity that lets us rewrite sin(x+h). That’s where we’ll pick up tomorrow....

Finish derivatives of the trigonometric functions.

Read section 3.5.

Next Lecture