The Product and Quotient Rules

Return to Course Outline

Previous Lecture

Questions?

The Product Rule

“The Product Rule” in section 3.3

Key Idea(s)

There’s a formula for derivatives of products (knowing this, you can look it up when you need it — and it’s given in the examples below, where you needed it).

Examples

Find the derivative of (2x² - x + 1)(x³ + 3x² - 2)

Once you identify “f” and “g” parts of this function, apply the product rule. The rest is multiplying out polynomials and simplifying:

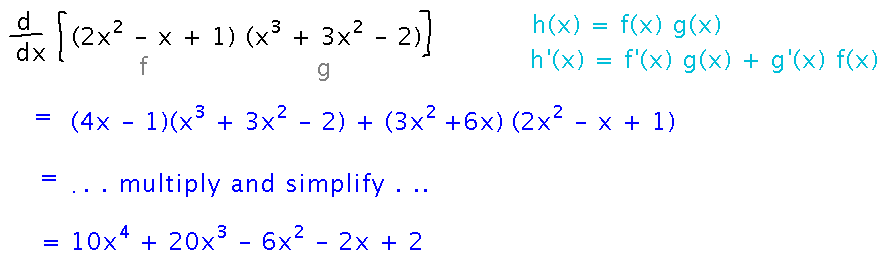
Suppose you know that h(x) = f(x)g(x), f(0) = 1, f’(0) = 3, g(0) = 2, g’(0) = -2. What is h’(0)?

You can use the product rule (and other differentiation rules) on the numeric values of derivatives at specific points as well as on derivatives of functions:

Antiderivatives?

A form of reverse product rule appears as “integration by parts” in calculus 2.

Quotient Rule

“The Quotient Rule” in section 3.3

Key Idea(s)

Formula:

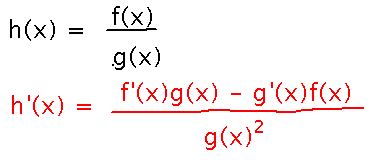
Examples

Find the derivative of x² / (2x + 1)

As with the product rule, identify “f” and “g,” plug them into the rule, and simplify:

What’s the derivative of (x² - 3x + 1)/x³?

This is very similar to the above example, except there are more opportunities to simplify at the end:

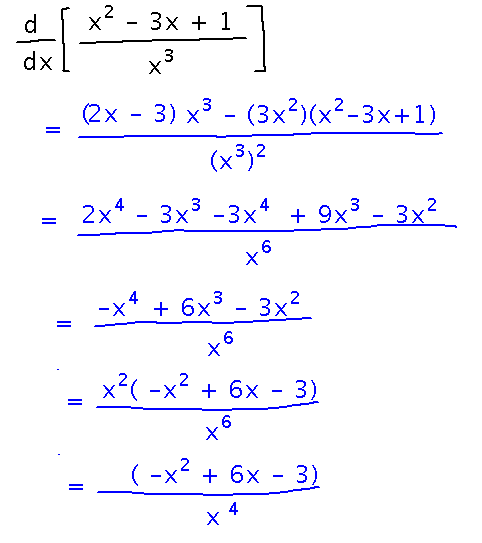
Antiderivatives?

No general rule

Power Rule

Could you use the original power rule on x^-2?

In fact, not the way it was presented, because the argument for its correctness assumed exponents were positive integers.

But now that we have the quotient rule, we can extend the power rule (which the book does, in an “Extended Power Rule” theorem) to negative exponents by treating x^-n as the quotient 1/xⁿ.

Next

Applications of derivatives as rates of change.

Read section 3.4.

Next Lecture