SUNY Geneseo Department of Mathematics

Infinite Limits

Thursday, September 12

Math 221 06
Fall 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

SI session this afternoon, 3:00 - 4:30, Fraser 104.

Questions?

Infinite Limits

“Infinite Limits” from section 2.2.

Key Idea(s)

Infinite limits can find vertical asymptotes

Limits can be infinite

What a vertical asymptote is

Infinite limit theorem comes from the formal definition of infinite limit, use it to find infinite limits.

Infinite Limit Theorem

lim_x→a f(x) = ∞ if for any alleged upper bound, M, on f(x), there is a tolerance δ such that whenever x is within δ of a, f(x) is actually greater than M.

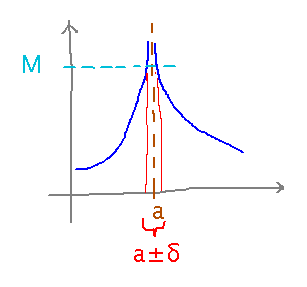
Graph rising above supposed upper bound M in a narrow region around x = a

lim_x→a f(x) = -∞ if for any alleged lower bound, N, on f(x), there is a tolerance δ such that whenever x is within δ of a, f(x) is actually less than N.

The parts of the theorem can be proven from these definitions.

So the key strategy for rigorously showing that a limit of f(x) is infinite is to put it into a form you can apply this theorem to, possibly supplemented by limit laws.

Examples

Find lim_x→1 x / (x-1)²

First use the product law to break this into a limit of x times a limit that the infinite limit theorem applies to. Then use that theorem.

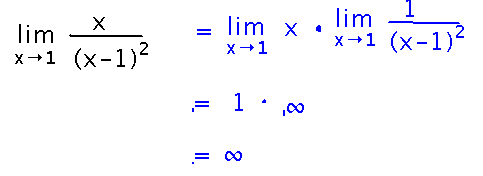
Factor x over x minus 1 squared into x and 1 over x minus 1 squared, the limit of the latter is infinity

Notice that at the end we used the idea that 1 × ∞ is infinite, which is true (infinity times any finite number is infinite), but in general you have to be careful about arithmetic involving infinity: infinity is not a number, and doesn’t always behave like one (for example, take the infinite number of even integers away from the infinite number of integers and you have the infinite number of odd integers, suggesting that ∞ - ∞ = ∞; but take the infinite number of integers away from the infinite number of integers and you have nothing left, suggesting that ∞ - ∞ = 0 too).

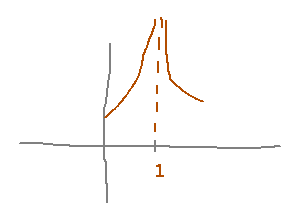
Knowing that this function has an infinite limit at x = 1 we also know it has a vertical asymptote there, which tells us something about the shape of its graph:

A graph rising toward infinity from both sides of x = 1

Find lim_x→2^- 1 / (2-x) and lim_x→2⁺ 1 / (2-x)

Here we use the two parts of the infinite limit theorem that apply to odd powers in the denominator. One yields -∞ and the other yields ∞, but notice that each applies to a limit from a different side.

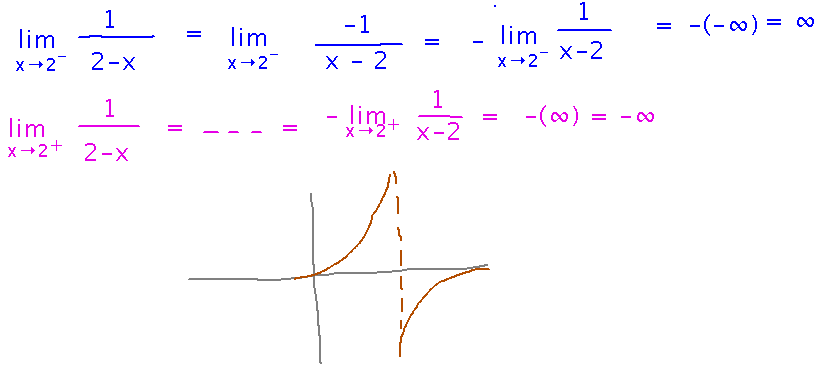
Two 1-sided limits, one positive infinity and one negative infinity

Continuity.

Read section 2.4.

Next Lecture