One-Sided Limits

Questions?

Problem set 2 grading is this Friday through next Tuesday.

Limits in Mathematica

The main relevant Mathematica function is Limit.

Here is a notebook that demonstrates its use.

One-Sided Limits

“One-Sided Limits” from section 2.2.

Key Idea(s)

Sometimes limits that don’t exist can be replaced by limits from above (the right) and below (the left). This also implies that there are such things as one-sided limits in the first place.

Notation:

Example

Find lim_x→0^- |x|/(2x) and lim_x→0⁺ |x|/(2x)

From trying some values of the function, it looks like the limits are -0.5 and +0.5. That’s also consistent with this graph that we made with Mathematica:

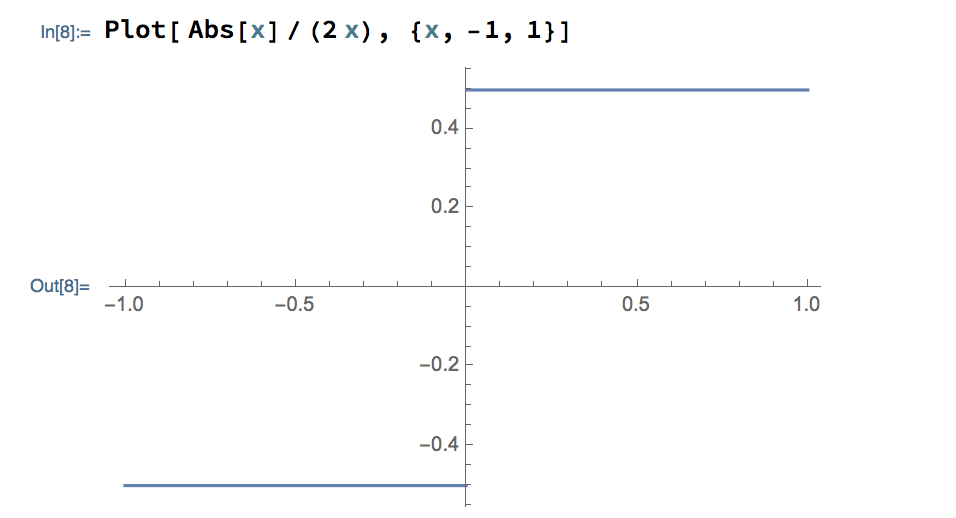
To get an analytical solution, realize that absolute value can be re-written according to whether x is positive or negative. This lets us turn the limits into things we can evaluate with limit laws and algebraic methods we already know.

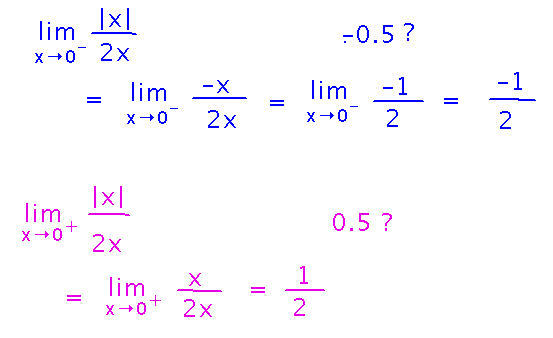
Does the corresponding 2-sided limit (i.e., lim_x→0 |x|/(2x)) exist? Why or why not? If so, what is it?

No, it does not exist, because the 1-sided limits are different on each side.

A Piecewise Function

Suppose g(x) is defined as (1) g(x) = x² - 1 if x ≤ 0, (2) g(x) = 2x - 1 if 0 < x ≤ 1, and (3) g(x) = x² + 1 if x > 1.

Does lim_x→0 g(x) exist? How about lim_x→1 g(x)?

Since there’s no common expression for g(x) on both sides of either limit, you have to break the limits into 1-sided limits and use the appropriate definition on each side. For x approaching 0, both 1-sided limits turn out to be the same, so the 2-sided limit exists.

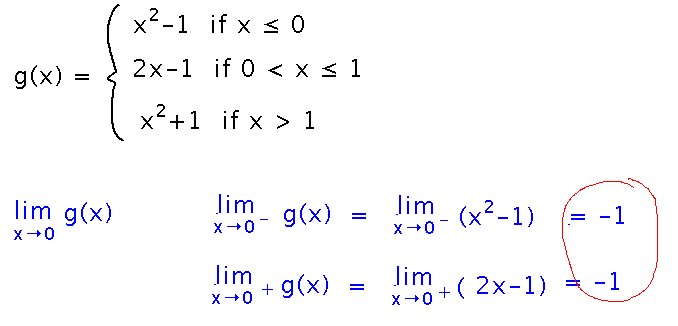
For x approaching 1, the 1-sided limits are different, so the 2-sided limit does not exist.

Key Idea

Use the side you’re approaching from to simplify the expression, especially removing things not handled by limit laws.

Next

Infinite limits.

Read the “Infinite Limits” subsection of section 2.2.