More on Formal Limits

Return to Course Outline

Previous Lecture

Misc

SI Sessions are in Fraser 104.

First is today, 3:00 - 4:30.

Questions?

The Formal Definition of Limit

“Quantifying Closeness” subsection of section 2.5, pages 194 & 195.

Reading

Yesterday, we decided that the book’s claims that

• “The statement |f (x) − L| < ε may be interpreted as: The distance between f (x) and L is less than ε.”
• “The statement 0 < |x − a| < δ may be interpreted as: x ≠ a and the distance between x and a is less than δ.”
• “The statement |f (x) − L| < ε is equivalent to the statement L − ε < f (x) < L + ε.”
• “The statement 0 < |x − a| < δ is equivalent to the statement a − δ < x < a + δ and x ≠ a.”

all make sense.

Let’s go on and look at the definition of “limit” itself.

Read through it piece by piece, stopping to make sure we understand each piece, thinking of examples where helpful, etc.

Use what we decided yesterday to give English understandings of the parts involving |f (x) − L| < ε and 0 < |x − a| < δ. This finally gives us an intuitive understanding of what ε and δ represent: tolerances around the proposed limit and the value x is approaching, respectively.

Linear Example

Suppose f(x) = 3x + 1; I claim lim_x→2 f(x) = 7

Find a δ that supports this claim for ε = 1

Knowing that ε = 1 gives us an interval around 7 (the proposed limit) in which 3x + 1 must lie, namely between 6 and 8. Then we can solve for x to find an interval around 2 in which x must lie. The distance between 2 and the ends of this interval is δ:

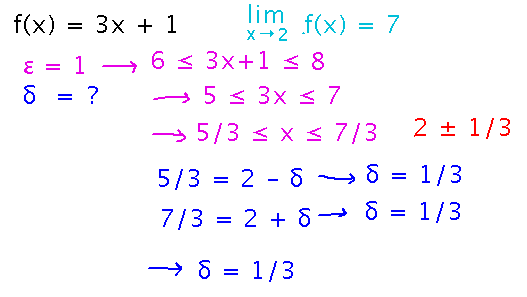
Next

Arithmetic of limits and using it to find them.

Read the “Evaluating Limits with the Limit Laws” and “Limits of Polynomial and Rational Functions” subsections of section 2.3.

Next Lecture