SUNY Geneseo Department of Mathematics
Wednesday, September 4
Math 221 06
Fall 2019
Prof. Doug Baldwin
Monday 6:00 - 7:30; Thursday 3:00 - 4:30
Room TBA — watch Canvas announcements
Now open, South 332
Hours are roughly…
See https://www.geneseo.edu/math/mlc for more info
A program of students advising students on the practicalities of academic life at Geneseo (study tips, navigating academic information systems, etc.)
Visit on a walk-in basis Monday - Friday, 10:00 - 3:00, Erwin 106.
They also run workshops.
See https://www.geneseo.edu/dean_office/academic-peer-mentors-0
Turn in problem set by meeting with me, some time between next Monday and Wednesday. Bring a written copy of your answers (a computer file we look at on your computer is fine) to the meeting for efficiency, although you don’t have to leave that copy with me.
“Quantifying Closeness” subsection of section 2.5, pages 194 & 195
Tips for reading at this level of detail:
It really is hard to make sense of this reading. So go through it point by point.
“The statement |f (x) − L| < ε may be interpreted as: The distance between f (x) and L is less than ε.” The key question to ask yourself here is “does this make sense to me, and why?” Think about f(x) and L on a number line to see why their difference is the distance between them; supplement the number line with concrete examples of what f(x), L, etc. might represent if it helps you understand them. The absolute value ensures that you still have a positive distance even if L is bigger then f(x). And ε (epsilon) is just another variable that stands for a number.
We spent 10 or 15 minutes understanding this one line, but that’s OK. Sometimes that’s what difficult reading takes, and taking the time be sure sure you have a really good understanding of it can pay off later.
“The statement 0 < |x − a| < δ may be interpreted as: x ≠ a and the distance between x and a is less than δ.” Again, ask yourself whether this makes sense, and why. The part about x ≠ a makes sense because 0 is less than x - a, but if x and a were equal their difference would be 0. The rest is just the distance between 2 numbers idea from the first claim. (δ is the Greek letter delta.)
“The statement |f (x) − L| < ε is equivalent to the statement L − ε < f (x) < L + ε.” Looking at some examples can help illustrate that this equivalence is reasonable.
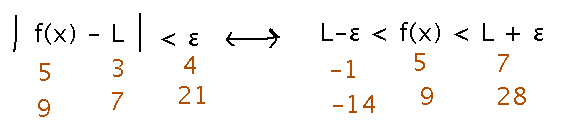
You can also work out algebraically why this must always be true. If you do that and write it out at the end of your problem set solution I’ll give a point of extra credit for it.
“The statement 0 < |x − a| < δ is equivalent to the statement a − δ < x < a + δ and x ≠ a.” Our examples from above help reassure us that the “a − δ < x < a + δ” part is reasonable (it’s just the previous point, with different variables), and the “x ≠ a” part makes sense as it did in the second point above.
Continue this careful reading with the actual definition of “limit.”
No new reading to do before class.