SUNY Geneseo Department of Mathematics
Thursday, August 29
Math 221 06
Fall 2019
Prof. Doug Baldwin
Please fill out Maddy’s survey re SI times
Section 2.1.
How clear was this section?
It varied, from not at all clear to very.
Suggestion: expect to read math (or other technical/difficult material) in several passes
Try looking for key ideas in Section 2.1…
Monday, we talked about Gallileo measuring how far a ball rolled in a given time, and discovering that distance y is proportional to the square of time, t. For simplicity, let’s assume y = t2.
We also saw how Gallileo could use his measurements to find average speeds over measured time intervals, but not instantaneous speeds.
Is there some idea from the reading that could be used to get better estimates of instantaneous speeds?
Ideas of rate of change and secant lines. Gallileo could find y values for 2 close-together t values, and the find the slope between those points.
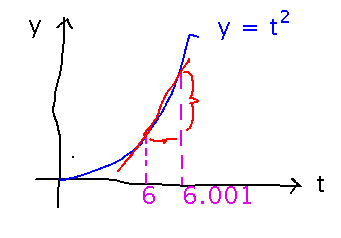
This is still an estimate, but Gallileo can make it as good as he wants by moving the t values he uses closer together.
Suppose in some strange alternate universe, Gallileo had a way to measure speed as a function of time, but not distance. Suppose that alternate-universe-Gallileo found that s = 2t, where s is speed and t is time.
What might this Gallileo do to find instantaneous distances (i.e., the distance the ball had rolled at specific t values)?
He can use areas. The reason is that there’s an easy formula for distance y in terms of speed s and time t if speed is constant: y = st. Speed is constantly changing in this case, so Gallileo can’t use this formula directly. But he could assume that speed is nearly constant over a small interval in t, and so multiply the speed at (say) the start of that interval by the width of the interval to get distance traveled during that interval. But this is equivalently multiplying the height of a rectangle under the graph of speed by its width, i.e., calculating the area of that rectangle.
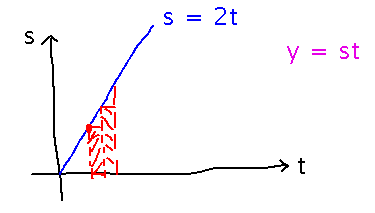
Either way you think of it, Gallileo then needs to find the areas aka distances for all the little intervals of t and add them up to get the total distance traveled.
What does this have to do with the reading?
It brings in the area problem. More intriguingly, it suggests that area is in some sense an inverse of slope, i.e., to reverse a distance-to-speed problem that involved estimating the slope of a curve, we solved a speed-to-distance problem by finding area under a curve. This inverse relationship between the two main problem areas of calculus really does hold up in general, and is captured in the so-called “Fundamental Theorem of Calculus.”
What do the two Gallileo scenarios have in common?
There were two central problems, slope and area
Both involved approximations, which became exact answers in the limit as intervals in t became shorter and shorter. In other words the idea of “limit” is a crucial tool for solving both problems.
And they turned out to be inverses of each other
The informal concept of “limit”
Read the “Intuitive Definition of a Limit” subsection of section 2.2
Please also bring a computer with Mathematica installed on it to class — I plan to start showing you some of the things Mathematica can do.