Work and Pumping

Return to Course Outline

Previous Lecture

Misc

Review Session

Tuesday, Dec. 12, 9:30 - 10:30 AM, Fraser 213 (our Thursday room).

You bring topics/questions you want to review.

Final

Thursday, December 14, 8:00 AM, in our MWF Sturges classroom (Sturges 223).

The exam will cover the whole semester, but emphasizing material since the second hour exam (e.g., optimization; the Fundamental Theorem; substitution; area, volume, and similar applications of definite integrals; etc.)

Roughly 2 to 2 1/2 times as long as the hour exams in terms of number of questions and design time. But note that you have roughly 4 times as long in terms of actual time, so there should be less time pressure.

The rules and format will otherwise be the same as on the hour exams, particularly the open-references and calculator rules.

I’ll bring donuts and cider.

SOFIs

Available from now through December 12.

Please fill them out — they’re useful to me in improving courses over time, especially written comments.

You get $1 / SOFI added to your printing account.

Get to the SOFI survey via Knightweb.

Questions?

Work Associated with Pumps

“Work Done in Pumping” subsection of section 6.5.

My Well House

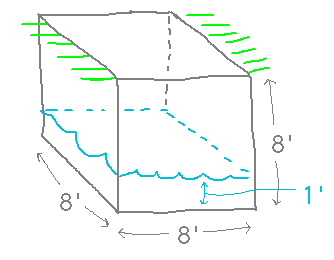
I have a well at home, which is located in an underground chamber about 8 feet on a side. Being underground, this chamber tends to fill up with ground water and every so often needs to be pumped out. How much energy does it take to pump out a foot of accumulated water?

From the reading on work and pumping, the following steps should apply to this problem:

1. Sketch the situation and define a coordinate system in which to describe it.
2. Find the weight (i.e., force) of a thin layer of the liquid as the volume of the layer times its density.
3. Multiply force by the distance lifted to get the work to lift this layer.
4. Sum the work for all layers — this is a Riemann sum.
5. Take the limit as the number of layers goes to infinity, and evaluate the resulting integral.

In this problem, a coordinate system with an origin at ground level and values increasing downward into the well house is helpful (step 1):

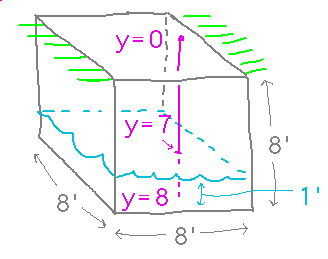
We know that work is the integral of force times distance, and this coordinate system gives us a way to talk about the relevant distances, namely the distances water has to be raised. They range from 7 feet for the uppermost water to 8 feet for the lowest. This basically takes care of the last 3 steps in the above procedure.

Step 2 in the procedure finds F(y), i.e. the force, for this integral. Think about a thin layer of water. Since in this problem that slice is a rectangle, its volume is its length (8 feet) times its width (8 feet) times its thickness (Δy, or as you take the limit, dy). Then its weight is its density times that volume; a typical density for water is around 62 pounds/cubic foot.

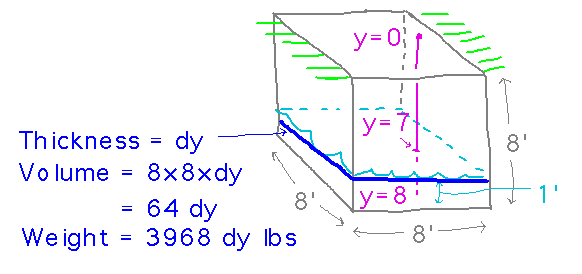
Now we can plug this weight into the integral and evaluate:

Parabolic Barrel

Briefly consider a case in which layer dimensions and density both vary: a barrel shaped like the parabola y = x² rotated around the y axis, containing a fluid whose density increases with increasing height:

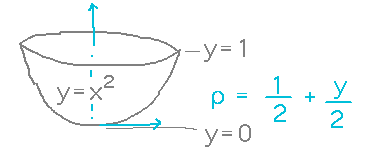
We can still use the ideas we’ve been developing, in particular slicing the barrel into layers and calculating the weight of each layer from its volume and density.

Take-Aways

Notice that the layers we used in these density problems are much like the slices we used to find volumes. Such connections are the big point here:

Integrating over thin slices is key to finding volumes, masses, work, etc., mostly depending on what you multiply the volume of each slice by.

Next Lecture