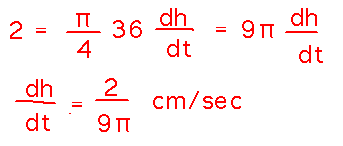SUNY Geneseo Department of Mathematics

Review

Tuesday, December 12

Math 221 05
Fall 2017
Prof. Doug Baldwin

Optimization?

How to set up problem 2 from homework 8 (given two poles with a wire from the top of one to the ground and then to the top of the other, where should the wire reach the ground to minimize its overall length?)

The first step is to simply draw the situation and introduce variables to describe key quantities.

20 foot and 10 foot poles with wire running from their tops to common point x units from the 20 foot pole

Now write expressions for the length of the wire.

L_1 = sqrt(400+x^2); L_2 = sqrt(100+(30-x)^2); L = L_1 + L_2

Since we’re trying to find the value of x that minimizes L, we want to find an x that makes dL/dx 0. Start by finding dL/dx, via repeated use of the chain rule.

dL/dx = x/sqrt(400+x^2) + (x-30)/sqrt(100+(x-30)^2)

From here you can simplify the expression for dL/dx and solve for it being 0.

Volume by Shells?

Two examples inspired by problems in the book. Both deal with the region between the graphs of y = x and y = x².

Example 1

In the first example, we want to know the volume of the shape produced by rotating this region around the line y = 2:

Thin half-moon-shaped region rotated up around y=2

Visualize how you would slice up the region so that rotating turns the slices into thin shells or cans around the rotation axis. In this case, the slices would have to be horizontal:

Half-moon region with thin slice across it

Now you can bring in the general equation for volume via a shell, which involves the radii and heights of the shells (note that in this problem “height” is really extent in the horizontal direction):

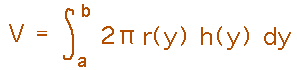
V = integral from a to b of 2pi r(y) h(y)

Finally, figure out the radius and height for this specific problem. Radius is just distance from the rotation axis, in this case 2 - y. Height is the distance between the two curves, √y - y in this case.

V = integral from 0 to 1 of 2pi (2-y) (sqrt(y)-y)

From here, evaluate the integral as you would any other to get a number for the volume.

Example 2

What if we rotate around the y axis?

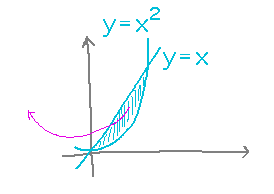
Thin half-moon-shaped region rotated around the y axis

This is similar to the first example, except that now the slices are vertical:

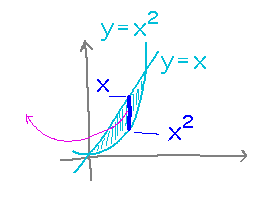
Half-moon-shaped region with a vertical slice

In the volume integral, the radius is distance from the y axis, or x, and the height of the slice is x - x² (since over this range of x values, x is greater than x²).

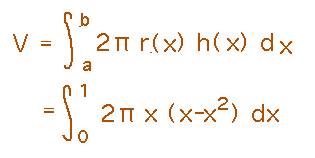
V = integral from 0 to 1 of 2pi x (x-x^2)

Related Rates?

An example related rates problem, courtesy of one of your “real-world math” extra credit submissions.

Consider a water dispenser serving water into one of those little cone-shaped paper cups. This particular cup is 8 cm high and has a top radius of 4 cm. The dispenser is pouring water in at a rate of 2 cc/sec. How fast is the water level in the cup rising when there is already 6 cm of water in it?

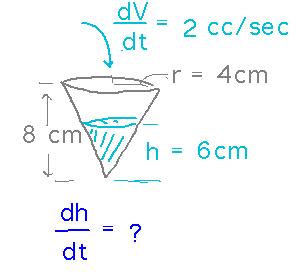
Cone 8 cm high and 4 cm radius filled with water to depth 6 cm

We know how fast volume is changing, and want to connect that to how fast depth is changing. So let’s see if the formula for the volume of a cone can make the connection.

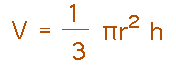
V = 1/3 pi r^2 h

This formula does indeed connect volume to depth, but also depends on radius. But the particular cone in this problem has a radius half the depth, and that will be true of all smaller cones within the large one by similar triangles. So replace r by h/2 to get...

V = 1/3 pi h^2/2 h = pi/12 h^3

Now we can differentiate this expression for volume, to get dV/dt (which we know is 2), and thanks to the chain rule, a dh/dt factor that represents what we want to know.

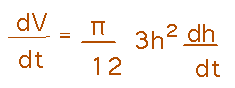
dV/dt = pi/12 3h^2 dh/dt

Finally, plug in the known numbers and solve for dh/dt:

2 = pi/4 times 36 times dh/dt so dh/dt = 2/9pi cm/sec

(No Next Lecture)