Misc
Review Session
Tuesday, Dec. 12, 9:30 - 10:30 AM, Fraser 213 (our Thursday room).
You bring topics/questions you want to review.
Final
Thursday, December 14, 8:00 AM, in our MWF Sturges classroom (Sturges 223).
The exam will cover the whole semester, but emphasizing material since the second hour exam (e.g., the Fundamental Theorem; substitution; area, volume, and similar applications of definite integrals; etc.)
Roughly 2 to 2 1/2 times as long as the hour exams in terms of number of questions and design time. But note that you have roughly 4 times as long in terms of actual time, so there should be less time pressure.
The rules and format will otherwise be the same as on the hour exams, particularly the open-references and calculator rules.
I’ll bring donuts and cider.
SOFIs
Available from now through December 12.
Please fill them out — they’re useful to me in improving courses over time, especially written comments.
Get to the SOFI survey via Knightweb.
Questions?
Mass and Density
The first subsection of section 6.5
Warm-Up
Find the mass of a section of thin wire between x = 1 and x = 3, if the linear density of the wire at position x is given by ρ(x) = x2 / 3 - 4x g/cm. (Notice that this is a completely arbitrary function, and accidentally gives negative densities over the interval [1,3]. This means the mass will be negative — we’ve apparently invented antigravity wire!)
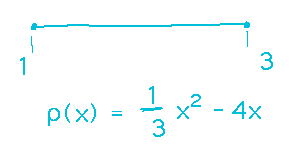
The reading gives a formula for mass from linear density:

This formula follows from the idea that mass equals density times volume. When the density varies, you can’t just multiply the two together, but you can break the volume into smaller and smaller sections, each of which has a more and more nearly constant density over it. Adding all the masses estimated for these sections gives a total mass. But this is a Riemann sum, and so in the limit as the number of sections goes to infinity it gives you this integral.
Now plug the density function into this integral, using the endpoints of the wire as the bounds, to get

Realistic Rod
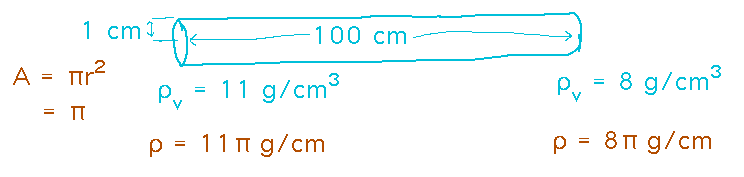
Textbook examples using functions chosen more for ease of integration than anything else don’t necessarily convince you that this technique is useful. So here’s a more physically realistic example (though still not one you couldn’t do by other means): Consider a 1 meter metal rod, 1 cm in radius, which is pure lead (volume density about 11 g/cm3) at one end and pure iron (volume density about 8 g/cm3) at the other, with the lead/iron blend changing linearly along the length of the rod. What’s the mass of the rod?

This problem doesn’t particularly fit the template given in the book. First, it has volume densities, not linear ones, and second there’s no function giving density in terms of x (indeed, there’s no x axis at all). To deal with the first problem, note that linear density is mass per unit of length, i.e., the weight of 1 cm of the rod. Since sections of the rod are cylinders, find this mass by multiplying the cross-sectional area of the rod by 1 to get volume, and then multiplying that volume by the volume density to get linear density:
Now you can come up with a linear density function by letting the lead end of the rod be at x = 0 and the iron end at x = 100. Then multiply the lead density by something that varies linearly from 1 when x = 0 to 0 when x = 100, and the iron density by something that varies linearly from 0 when x = 0 to 1 when x = 100. (1 - x/100) and x/100 serve well as these “somethings”:
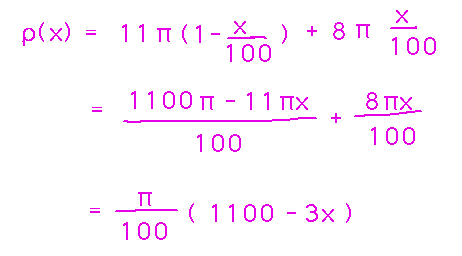
Now there’s a linear density function, and some bounds to integrate it over. Do so:
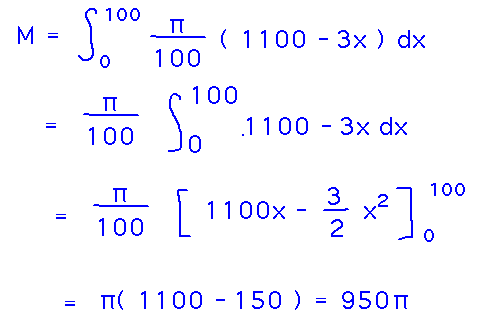
Take-Aways
Find masses from linear densities by identifying the density function and the bounds within which it applies, then integrating it over those bounds.
Next
Look at work as an integral.
- Read the “Work Done by a Force” and “Work Done in Pumping” subsections of section 6.5.