SUNY Geneseo Department of Mathematics

Arc Length

Wednesday, December 6

Math 221 05
Fall 2017
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Review Session?

Do you want to have a roughly 1-hour review session sometime in the morning of study day (Dec. 12)?

You bring topics you want to review.

I will try to find a room and time and let you know tomorrow.

Final

Thursday, December 14, 8:00 AM, in our MWF Sturges classroom.

The exam will cover the whole semester, but emphasizing material since the second hour exam (e.g., the Fundamental Theorem; substitution; area, volume, and similar applications of definite integrals; etc.)

Roughly 2 to 2 1/2 times as long as the hour exams in terms of number of questions and design time. But note that you have roughly 4 times as long in terms of actual time, so there should be less time pressure.

The rules and format will otherwise be the same as on the hour exams, particularly the open-references and calculator rules.

I’ll bring donuts and cider.

SOFIs

Available from now through December 12.

Please fill them out — they’re useful to me in improving courses over time, especially written comments.

Get to the SOFI survey via Knightweb.

Questions?

Arc Length

Warm-Up

How long is the curve y = 4x3/2 - 1 between points (0,-1) and (1,3)?

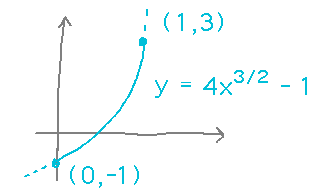
Graph of y = 4x^(3/2) - 1 from x = 0 to x = 1

Reading ideas: there is a formula for arc length in terms of a varying x. The a and b bounds in this formula are values of x, because that’s the variable in terms of which the integral is expressed.

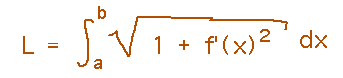
L = integral from a to b of sqrt(1 - fPrime(x)^2)

To use this formula, identify the function, f, and it’s derivative:

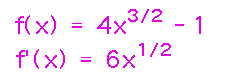
f(x) = 4 x^(3/2) - 1; fPrime(x) = 6x^(1/2)

Then plug the derivative (squared) into the formula and integrate:

Integral from 0 to 1 of sqrt(1+36x) approximately equals, via substitution u = 1+36x, 4.15

This superficially strange looking formula actually comes from adding up (in a Riemann sum) the lengths of short straight segments along the curve, and then factoring a Δx2 out of the square root.

Function graph divided into segments

Sine Curves

How long is a sine wave?

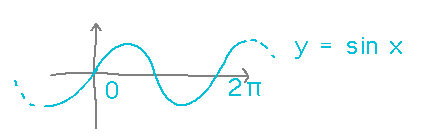
Graph of y = sinx over slightly more than 0 to 2 pi

Follow the same procedure as before, i.e., identify f and its derivative, then use the formula:

L = integral from 0 to 2pi of sqrt(1+cos^2(x))

This time the integral can’t be evaluated by hand, so use muPad or some other CAS. But even muPad doesn’t handle it well...

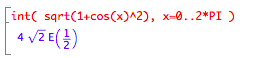
int( sqrt(1+cos(s)^2), x=0,2*PI) is 4 sqrt(2) E(1/2)

What muPad is trying to say with “E(1/2)” is that this is a so-called “elliptic integral,” a kind of integral that originally arose in connection with finding lengths around ellipses, and which is known not to have a symbolic closed form. But in cases like this muPad (and other symbolic math systems) can evaluate the integral numerically, essentially by calculating a close approximation to the Riemann sum.

numeric::int( sqrt(1+cos(x)^2), x=0.2*PI) is about 7.64

Next

Some physical uses of integration

Read the “Mass and Density” subsection of section 6.5 of the textbook.

Next Lecture