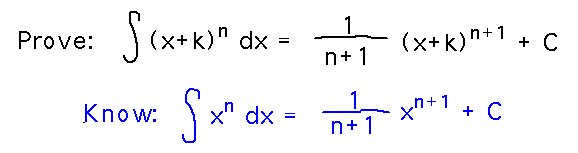
SUNY Geneseo Department of Mathematics

Volume by “Washers”

Wednesday, November 29 - Thursday, November 30

Math 221 05
Fall 2017
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

End of Semester

Final

Thursday, December 14, 8:00 AM, in our MWF Sturges classroom.

The exam will cover the whole semester, but emphasizing material since the second hour exam (e.g., the Fundamental Theorem; substitution; area, volume, and similar applications of definite integrals; etc.)

Roughly 2 to 2 1/2 times as long as the hour exams in terms of number of questions and design time. But note that you have roughly 4 times as long in terms of actual time, so there should be less time pressure.

The rules and format will otherwise be the same as on the hour exams, particularly the open-references and calculator rules.

I’ll bring donuts and cider.

SOFIs

Please fill them out — they’re useful to me in improving courses over time, especially written comments.

Math Learning Center Survey

You may have gotten an email invitation to participate in a survey about the MLC; if so, please do the survey to help the MLC improve its tutoring.

Questions?

Problem Set 10, Question 1

You can use the basic power rule for antiderivatives, but the problem is that you only know it applies to variables raised to a power, e.g., xn, not to expressions of the form (x+k)n.

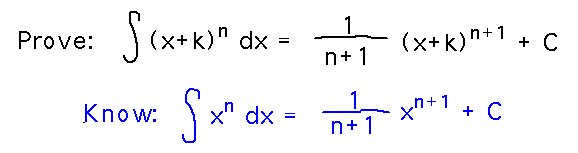
Prove integral of (x+k)^n = 1/(n+1) (x+k)^(n+1), knowing integral of x^n = 1/(n+1) x^(n+1)

As implied in the question, a substitution would be a good way to connect the power rule for variables to one for variables plus constants.

Problem Set 10, Question 3.4

The most obvious substitution is u = 1 + y. So try doing it and see where it gets you, especially noting that u = 1 + y also means that y = u - 1.

Integrate y^2 sqrt(1+y) by letting u = 1+y so integral becomes integral of (u-1)^2 sqrt(u)

Slices

Teacup

The parabolic teacup from Monday turned out to have volume

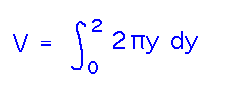
V = integral from 0 to 2 of 2 pi y dy

What is the numeric value of this integral?

Integral of 2 pi y from 0 to 2 = 4 pi

Take-Aways

To find the volume of some region R via slicing...

Washers

The last subsection of section 6.2.

Warm-Up

Take the region between the curves y = x2 and y = √x and rotate it around the x axis. What is the resulting volume?

Diagonal football-shaped region spun around a horizontal axis

Maybe you could find the volume enclosed by rotating the upper curve (√x in this case), and subtract from it the volume enclosed by rotating the lower curve (x2).

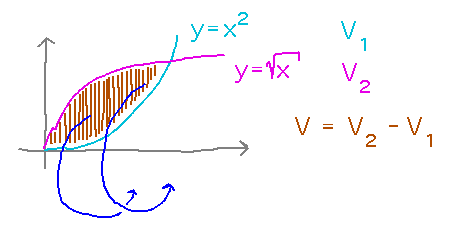
Spun region's volume is volume of region from spinning sqrt(x) minus volume from spinning x^2

This isn’t a bad idea — to find a simple way to carry it out, notice that both V1 and V2 can be calculated as integrals of circular slices.

Slice of spun region has area pi x - pi x^4

Now the volume of the shape we really want is the difference of the integrals, which is the integral of the difference, and out of which we can factor the constant π.

V_2 - V_1 = pi times integral from 0 to 1 of x - x^4

The integral is just the integral of the difference of the radii squared, which is the difference of the function values squared. So if f1 defines the inner surface of a hollow shape and f2 the outer surface, the volume of that shape via the washer method is...

V = pi times integral from a to b of f_2(x)^2 - f_1(x)^2

So now finish this example:

Integral from 0 to 1 of x - x^4 = 3/10 pi

Tori

What is the volume of a torus (and of my bicycle inner tube in particular)?

A torus is a tube bent into a circular shape, e.g., an inner tube or a donut. The main measures of its shape are the radius of the tube (r), and the radius of the circle it’s bent into (R).

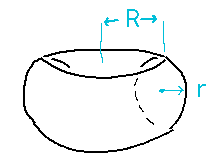
A tube of radius r wrapped in a circle of radius R

Put the torus in a coordinate system to make it easy to describe mathematically. Having the origin at the center of the torus and the middle of the tube at y = 0 works well.

Section of tube circling around xy coordinate system

To find volume using the washer method, we need to think of the torus as a set of washer-shaped layers. Then the volume will be the integral over an appropriate y interval of the difference of the squares of the washer radii (based on the idea that the area of a washer is the area of a circle of the washer’s outer radius minus the area of the circle inside the washer).

Washer with radii r_2, r_1; V = pi times integral from a to b of r_2^2 - r_1^2

For the torus, use washers perpendicular to the y axis and running across the tube. The Pythagorean theorem lets you figure out half the width of each washer, from which the inner and outer radii can be computed.

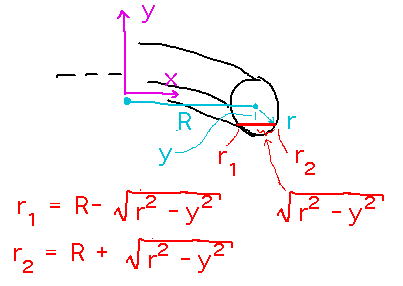
Section of torus with line at height y through it; half length of line is sqrt(r^2-y^2) so r_1 = R - sqrt(r^2-y^2), r_2 = R+sqrt(r^2-y^2)

Using these formulas for r1 and r2, and realizing that y ranges from -r to r, we can set up and simplify the integral:

Integral from -r to r of r_2^2 - r_1^2 simplifies to 4 pi R times the integral from -r to r of sqrt(r^2-y^2)

We don’t have techniques for integrating this, but that’s where technological tools help in a big way:

muPad defining f := sqrt(r^2-y^2) then finding int(f,x=-r..r)

The final expression for volume, for any torus, is

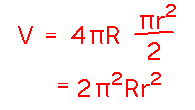
V = 2 pi^2 R r^2

In the specific case of my inner tube, R is about 12.5 inches and r is about 0.5 inches, for a volume of around 61.7 cubic inches.

Take-Aways

The washer method is a variation on the slice method.

To use washers...

  1. Identify a way of slicing the volume you want to find into washer-shaped slices. Call the inner and outer radii of the washers r1 and r2, respectively. Usually both radii are functions of some variable.
  2. Integrate r22 - r12 over the appropriate range of values of the variable.
  3. Multiply the integral by π. The product is the volume you want.

Next

Volume by shells

Read section 6.3 of the textbook (for Friday).

Next Lecture