Misc
Colloquium
Today’s talk is in Newton 214.
Final
Thursday, December 14, 8:00 AM, in our MWF Sturges classroom.
The exam will cover the whole semester, but emphasizing material since the second hour exam (e.g., the Fundamental Theorem; substitution; area, volume, and similar applications of definite integrals; etc.)
Roughly 2 to 2 1/2 times as long as the hour exams in terms of number of questions and design time. But note that you have roughly 4 times as long in terms of actual time, so there should be less time pressure.
The rules and format will otherwise be the same as on the hour exams, particularly the open-references and calculator rules.
I’ll bring donuts and cider.
SOFIs
Available from now through December 12.
Please fill them out — they’re useful to me in improving courses over time, especially written comments.
Questions?
Volume by Shells
Section 6.3
Explore the basic idea in connection with the torus (although the integral in this case will be much more complicated than the one we found via washers).
Instead of slicing the torus into horizontal washer-shaped disks, consider instead dividing cross-sections through the tube into vertical rectangles:
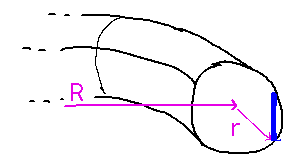
When circulated around the whole torus, these rectangles define cylindrical shells:

The volume of a cylindrical shell like this of radius r, height h, and thickness t is 2πrht. If we divide the torus into many such shells, we can add up all their volumes to find the volume of the torus.

This sum is a Riemann sum! We can turn it into an integral by taking the limit as the number of cylinders grows to infinity, and get the shell formula for the volume of a surface whose height is f(x):
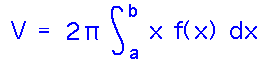
Next
Example(s) of computing volume via cylindrical shells.