SUNY Geneseo Department of Mathematics
Friday, September 29 - Monday, October 2
Math 221 05
Fall 2017
Prof. Doug Baldwin
Next Thursday (Oct. 5), in regular room
Covering material since the beginning of the semester, e.g., limits, derivatives, rules and laws for finding limits and derivatives, the chain rule, implicit differentiation, etc.
3 - 5 short-answer questions.
You’ll have the whole class period to do the test.
Open book, open notes, open computer/calculator, but closed person.
Section 3.6
Example. Find d/dx (3x+1)200
Reading idea: The power rule for compositions: if h(x) = gn(x) = (g(x))n, then h′(x) = ngn-1(x) g′(x).
From this rule, d/dx (3x+1)200 = 200(3x+1)199 × 3 = 600(3x+1)199.
Example. Find f′(x) if f(x) = sin2x cos2x = (sinx)2(cosx)2
Reading ideas: You’ll need to take derivatives of trig functions. You’ll also need the chain rule: if h(x) = g( f(x) ) then h′(x) = g′( f(x) ) f′(x).
Example. Find d/dt tan( √(t2-t) )
This uses the chain rule twice because there are 3 functions (tan applied to square root, and square root applied to t2-t):
Example. Find d2y/dx2 if y = sin(x3)
This is a second derivative, i.e., a derivative of a derivative.
Take-Aways. The chain rule formula (g′(f(x)) f′(x)) is vital when differentiating functions applied to other functions.
The chain rule can be, and often is, used in combination with other rules.
The chain rule is even used with itself, to differentiate compositions of compositions of functions.
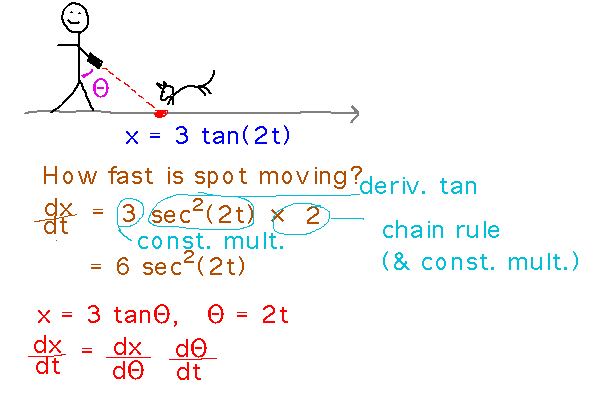
Recall the laser pointer example from the trigonometric derivatives lecture, but suppose I’m turning my wrist at a rate of 2 radians per second so that the spot’s position at time t is given by x = 3 tan(2t). How fast is the spot moving?
Imagine you’re walking along a road trying to get reception for your phone. There’s a cell tower a mile away from the road, and a mile down it. If you’re walking at a speed of 4 miles per hour, how fast is your distance to the tower changing?
Take-Aways. Thinking of the chain rule as dealing with situations in which there is an intermediate variable (Θ in the laser pointer example) lets you see it as correcting for different units in different derivatives. This also lets you state the chain rule in Leibniz notation, which may be easier to remember because it looks like “canceling out” the intermediate variable.
See handout.
Implicit differentiation.