Derivatives of Trigonometric Functions

Return to Course Outline

Previous Lecture

Misc

Exam 1

Next Thursday (Oct. 5)

Covering material since the beginning of the semester, e.g., limits, derivatives, rules and laws for finding limits and derivatives, the chain rule, implicit differentiation, etc.

3 - 5 short-answer questions.

You’ll have the whole class period to do the test.

Open book, open notes, open computer/calculator, but closed person.

Questions?

Derivatives of Trigonometric Functions

Section 3.5

Examples

Find d/dx (2 sinx cosx) = 2 d/dx( sinx cosx ).

Reading ideas: Use the rules for trigonometric derivatives and the rules we’ve seen earlier.

d/dx sinx = cosx

d/dx cosx = -sinx

Solution: d/dx (2 sinx cosx) = 2 ( sinx (-sinx) + cosx cosx ) {product rule & derivatives of sin and cos}

= 2( cos²x - sin²x )

Laser Pointer. Suppose I’m standing at x = 0 holding a laser pointer 3 feet off the floor, and tilting it in such a manner that at time t the point of light hits the floor at x = 3 tan t. How fast is the point moving?

Remember that velocity is the rate of change (i.e., derivative) of position.

Reading ideas: d/dx tan x = sec²x.

Take-Aways. You now have a bunch of new rules for differentiating trigonometric functions.

But the new rules need to be used with older ones in most cases.

Proofs

Fix typos in the proof that d/dx sin x = cos x.

“cos xh” on the 4th line should be “cos h,” as can be determined by checking the factoring from the previous line.

Reference to “cosh h” at the top of the page should be “cos h.”

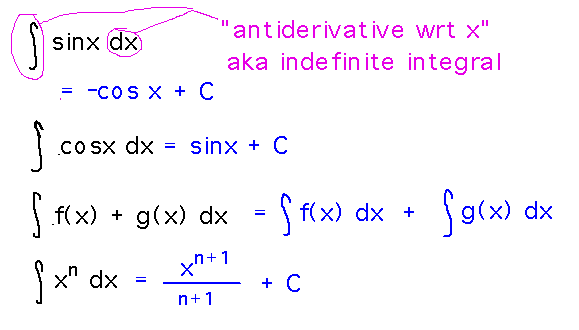
Antiderivatives

Rules for antiderivatives of sin x, cos x.

Other Rules. You informally know that an antiderivative of f is a function whose derivative equals f. Can you turn some of the other differentiation rules into rules for finding antiderivatives?

Next

The chain rule.

Read section 3.6.

Next Lecture