Geneseo Math 221 05 Implicit Differentation

Implicit Differentiation

Section 3.8

Note that muPad’s plot command plots implicit functions as well as explicit ones:

plot( x^3 + y^3 - 3*x*y ) plots a

Example. Find dy/dx if 4x² + y²/4 = 1.

Reading ideas: The basic process for implicit differentiation is...

Differentiate both sides of the equation with respect to x (or another variable of interest). This will involve the chain rule wherever terms refer to other variables, and may involve any of the other differentiation rules we’ve seen.
Solve the resulting equation for dy/dx (or other derivative of interest). In particular...
1. Isolate dy/dx terms on one side of the equation.
2. Factor out the dy/dx.
3. Divide both sides by the non-dy/dx factor.

Using these ideas to find dy/dx when 4x² + y²/4 = 1:

Implicit differentiation gives dy/dx = -16x/y

Example. Use implicit differentiation to find dy/dx if x/y = 1.

Implicit differentiation finds dy/dx = y/x

Take-Aways. Implicit differentiation lets you find derivatives even without having an equation of the form y = ....

There’s a pretty well defined process for implicit differentiation (see above).

The chain rule is always central to implicit differentiation. Other rules can come into play too.

Example. Find an equation for the line tangent to x²/10 - y²/9 = 1 at (10,9).

Use the point-slope equation for a line, (y - y₀) = m(x - x₀), where (x₀,y₀) = (10,9) and m = dy/dx.

Notice that implicit differentiation could find several derivatives, in this case dy/dx or dx/dy (the rate at which x changes with changes in y). You may need to decide which is the useful one for a particular problem.

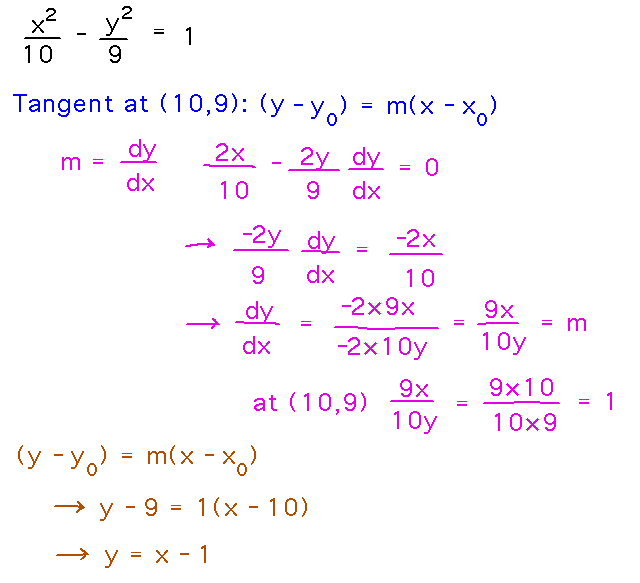
Implicit differentation finds slope of tangent = 9x/10y = 1

Take-Away. Implicit differentiation as a step or method within solving some larger problem.

(After the exam.)

Related rates.

Read section 4.1