SUNY Geneseo Department of Mathematics

Derivatives at a Point

Monday, September 18

Math 221 05
Fall 2017
Prof. Doug Baldwin

Questions?

Derivatives at a Point

Section 3.1

Typo. Practically the first paragraph about tangent lines has a typo regarding h. What is it and what should the text say?

The value of h needn’t be close to a. Rather, the idea is that h is small, i.e., close to 0.

Secant is close to tangent when h is small

Example. Find the derivative of f(x) = 7x - 3 at x = 2. In other words, what is f′(2)?

Reading ideas: Use the formula for f′(a), either the version in terms of x approaching a or the version in terms of h approaching 0.

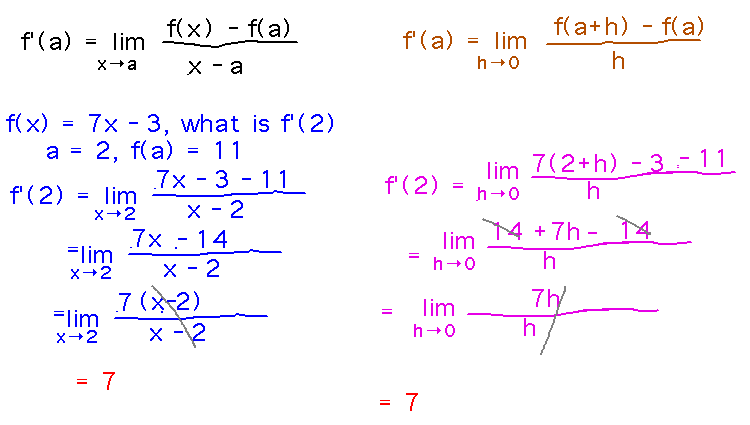
Limit as points get close together is 7

Could you also keep a as the variable and work out a general f′(a) = 7?

Yes, and in fact that’s how you get derivatives as functions, not just as things to calculate in isolation for individual points.

Limit as h approaches 0 of (f(x+h)-f(x))/h = 7

Example. Suppose you’re moving in such a way that your speed at time t is given by s(t) = 3√t feet per second. How fast is your speed changing when t = 1?

Reading ideas: derivatives are rates of change, so the answer to this question is s′(1).

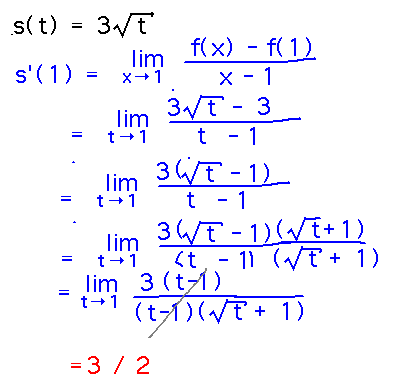
Limit as x approaches 1 of (3sqrt(x) - 3sqrt(1))/(x-1) = 3/2.

Take-Aways. The most important thing in this section is the definition of the derivative at a point as a limit (or more accurately, either of two equivalent limits).

The idea that a derivative is a rate of change is the source of a lot of the real-world importance of derivatives.

Problem Set

See handout.

The derivative as a function.

Read section 3.2

Next Lecture