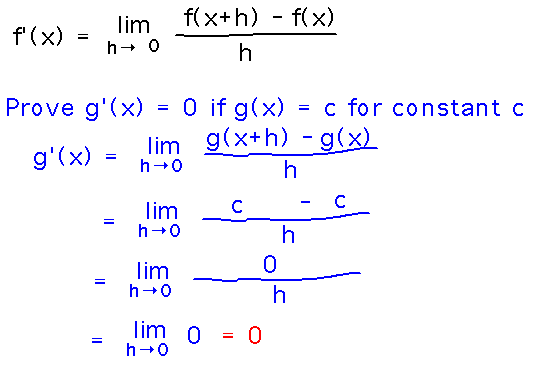
SUNY Geneseo Department of Mathematics
Wednesday, September 20
Math 221 05
Fall 2017
Prof. Doug Baldwin
Handout for problem set 3
Section 3.2
Rule. Prove that if f(x) = c for any constant c, then f′(x) = 0.
Reading ideas: use the definition of the derivative as a function.
Take-Away. There are rules for finding derivatives, with proofs from the definition.
Example. Find f′(x) if f(x) = x/2 - 3.
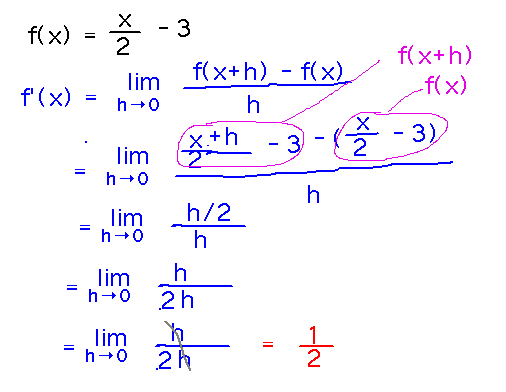
Example. Find dy/dx if y = (x+1)2.

Reading ideas: There are several notations for derivatives, including dy/dx, f′, etc.
Take-Aways. The main idea in this section is the limit definition of the derivative as a function; these examples help you practice what that definition means.
These examples also demonstrate several notations for derivatives.
Intuitive Derivatives. The banging outside our classroom sounds like a digger breaking up pavement by raising its bucket and then dropping it on the pavement over and over. Imagining that happening, what can you say about the derivative of the bucket’s height?
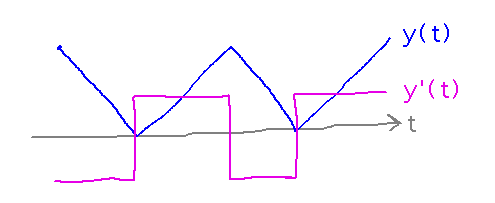
Observation: the derivative we’re looking for here is the speed or velocity of the bucket, i.e., velocity is the rate of change (derivative) of position.
Another observation: cyclic functions tend to have cyclic derivatives. We’ll see more of this when we look at derivatives of trigonometric functions.
Take-Aways. The value of a derivative corresponds to changes in the function, notably negative derivatives occur where the function is decreasing and positive where it is increasing.
Rules for finding derivatives.
Read section 3.3
Please bring muPad to class.