SUNY Geneseo Department of Mathematics

The Squeeze Theorem

Friday, September 15

Math 221 05
Fall 2017
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Trig Review

Presented by the Math Learning Center

Wednesday, September 20, 2:30 PM

Welles 26

Questions?

Proofs about Limits?

Problem set questions that ask for “proofs” about limits should use epsilon/delta proofs, as in yesterday’s class.

Problem Set Question 6?

Consider the equation F = G m₁m₂ / r²

As r approaches 0, this approaches ∞, so the actual values of G, m₁, and m₂ don’t matter as long as they’re constant

Problem Set Question 2?

Use limit laws or algebra to get the answer rigorously.

But a table of values, or the graph the question asks for, can be good ways to guess what the laws and algebra should be used to show.

The Squeeze Theorem

Subsection “The Squeeze Theorem” of section 2.3

The Basic Idea

Example. Use the squeeze theorem to show that lim_x→1x^√2 = 1.

Reading ideas: Even the theorem itself isn’t clear.

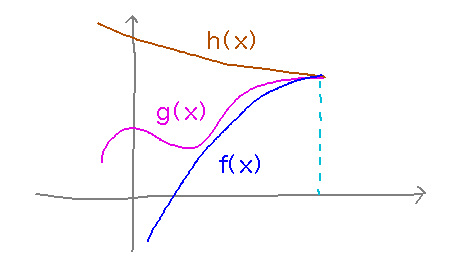
A visual explanation:

g(x), f(x) and h(x) all come to the same value if f(x) = h(x) and g(x) is in between f(x) and h(x)

Take-Away. if function g lies between functions f and h, and f and h have the same limit at some point, then since g lies between them it must have that limit at that point too.

Here’s how to use this idea to show that lim_x→1x^√2 = 1:

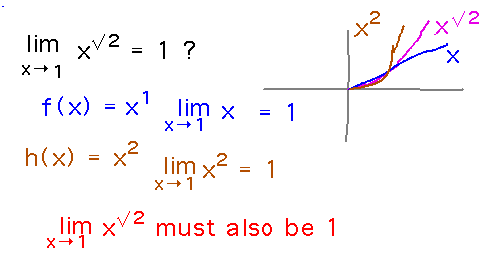
x^sqrt(2) squeezed between x and x^2 to a limit of 1 at 1

As a technical point, the book states the theorem in a way that requires f(x) ≤ h(x) at all points in some interval around a (the x value you want the limit at). This means the graphs of f(x) and h(x) can’t cross at a, although in practical cases they often do. To handle this really right you should separately use squeezing to show a limit as x approaches a from below, and a limit as x approaches a from above, switching the roles of f and h in the two squeezes. Assuming the 1-sided limits are equal, use that fact to conclude that the 2-sided limit(s) are also all equal.

Why This Matters

The squeeze theorem is a valuable tool for evaluating limits such as of trigonometric functions that don’t lend themselves to formal evaluation by the methods we’ve seen so far.

Example. Finish the proof that lim_x→0 sinΘ/Θ = 1 by filling in the details behind the “By applying a manipulation similar...” sentence.

It’s not clear what’s going on in that proof either. Especially what role the unit circle plays, and where the original inequality whose parts all get divided by sinΘ is.

Here are some explanations, with reference to the unit circle diagrams in the text (e.g., Figures 2.29 or 2.30):

First, radians as an angle unit have the property that 1 radian is the angle needed to make the length of the subtended part of a circle equal to the circle’s radius. More generally, this means that an angle of Θ radians subtends an arc of length Θ (measured in units of the circle’s radius). So a unit circle means that angle Θ subtends an arc of length Θ.
The unit circle also means that if you draw a line making angle Θ with the x axis out to the circle (see textbook figure 2.29), the length of a second line from the point where the first line intersects the circle perpendicularly down to the x axis is sinΘ (from the definition of sinΘ as “opposite over hypotenuse”, with the hypotenuse here being of length 1).
And furthermore, if you extend that line at angle Θ until it intersects a perpendicular coming up from the x axis at x = 1, that intersection happens at y coordinate tanΘ (again from the definition of tanΘ as “opposite over adjacent,” with the adjacent side now being of length 1). See textbook figure 2.30.
Since the line of length sinΘ is shorter than the arc it subtends, which is shorter than the line of length tanΘ, we have sinΘ < Θ < tanΘ. This is the inequality that the book then divides by sinΘ to get 1 < Θ/sinΘ < 1/cosΘ. Taking the reciprocals of all parts gives 1 > sinΘ/Θ > cosΘ, which is in a suitable form for applying the squeeze theorem to get a limit of sinΘ/Θ.
All of the above assumed that Θ is positive, i.e., the points and lines we’re dealing with lie in the first quadrant. As a result, the limits in the squeeze theorem are limits as x approaches 0 from the right. If Θ is negative, i.e., the points and lines lie in the fourth quadrant, things change slightly because while Θ < 0, lengths are always positive, and so the length of the arc subtended by angle Θ is -Θ (remember that Θ is negative, so -Θ is a positive number). Applying the ideas above to this situation is basically what the book referred to with the “applying a manipulation similar...” phrase.

Introduction to derivatives.

Read section 3.1.

Next Lecture