The Formal Definition of Limit

Return to Course Outline

Previous Lecture

Misc

PRISM Welcome Back Social

Thursday (i.e., today) afternoon, 5:00 PM

Fraser lounge

Pizza, people, etc.

GROW STEM

Catherine Cerulli (URMC), “Creating a Career Based on Values”

Thursday, 4:00 - 5:00, Newton 204

Questions?

The Formal Definition of Limit

Section 2.5

Examples

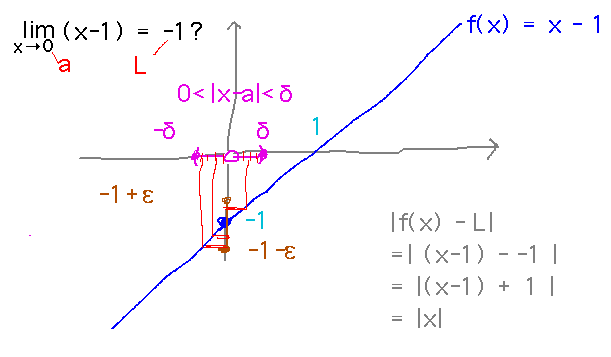
Prove that lim_x→0 (x-1) = -1.

Also sketch a graph showing how the formal definition of limit fits into this problem and what has to be done to finish the proof.

Reading ideas: Definition of limit -- lim_x→a f(x) = L if for every ε > 0 there exists a δ > 0 such that if 0 < | x - a | < δ then | f(x) - L | < ε

Essentially this says that no matter how tiny an interval around L you want to be in, there’s an interval around a that will put f(x) into the interval around L.

Algebraic proof:

1. Come up with δ
2. Prove that this δ works, i.e., if 0 < |x-a| < δ then | f(x) - L | < ε

Applying these ideas to the example:

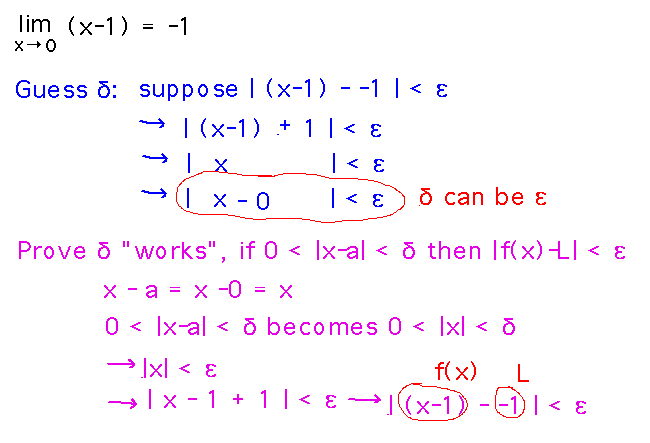
Take-Aways. Often proving that a δ you deduced from | f(x) - L | < ε “works” is just a matter of checking that the logic you used to find δ works in reverse.

Prove that lim_x→1 (3x+7) = 10.

Use similar ideas to what we did above. Notice at the end how the | f(x) - L | < ε requirement is equivalent to saying “f(x) lies within ± ε units of L.”

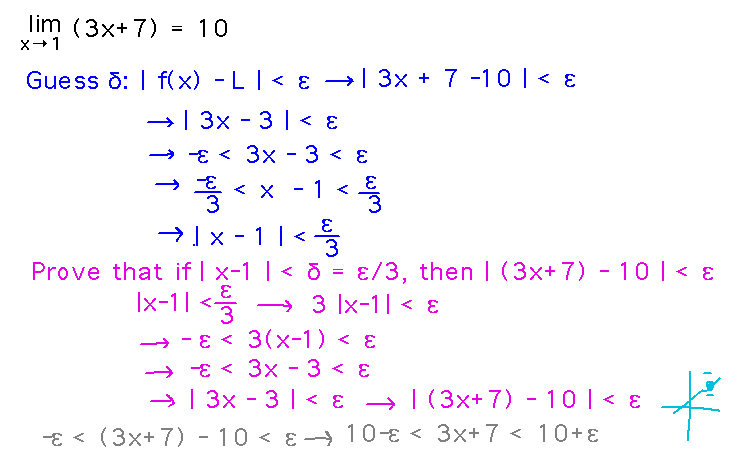
Next

The Squeeze Theorem.

Read “The Squeeze Theorem” subsection of section 2.3

Next Lecture