Continuity

Misc

GROW-STEM

Geneseo Reaching Out to Women and Under-Represented Groups in STEM Fields.

First event is this week:

Catherine Cerulli, URMC

“Creating a Career Based on Values”

Thursday (Sept. 14), 4:00 - 5:00

Newton 204

Problem Set 2

Beware that many questions have several subquestions not explicitly labeled as “parts.”

Questions?

Questions from Day 1

What is the number counting to? Maybe toward 10?

• The number is a function of time, f(t).
• So the answer to this question rests on what lim_t→∞f(t) is.

Is there a correlation between the pictures?

What are “yes” & “no” answers to? Which direction the bar moves?

Did the red line start at 0?

Is the red line ever going to overlap itself?

• The radius is function of time, r(t)
• So here we have another limit as t approaches infinity, lim_t→∞r(t)

Is the red figure really a 2D view of a 3D shape?

Is the number the radius of the red figure?

Limits are a useful tool for answering some of these questions. At this point you know enough about limits to appreciate that, but unfortunately we don’t get to limits as x approaches infinity ’til chapter 4. We’ll come back to these questions then.

Continuity

Section 2.4

Horizontal Lines and (Dis)Continuity

I have this feeling that when I talk to students about continuous functions, some of them think there’s a horizontal line test to recognize continuous functions. There isn’t, but let’s think a bit about whether there could be.

Note: The horizontal line test is really a test to see if a function is 1-to-1.

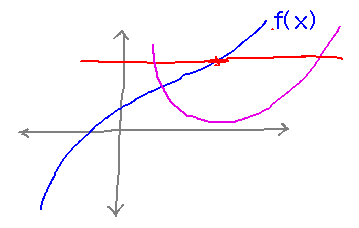
A Supposed Discontinuity Test: If there is some horizontal line segment parallel to the interval (a,b) on the x axis such that the graph of f(x) lies below the segment at some point(s) and above it at other(s), but the segment never intersects the graph of f(x), then f is discontinuous on (a,b).

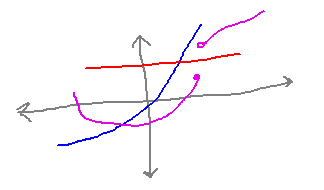
Show that this test is valid, i.e., any function that passes it really is discontinuous on (a,b).

Reading ideas:

• Discontinuities can be jump discontinuities (limits of f exist from each side but are unequal). Magenta curve above is an example.
• Discontinuities can be removable discontinuities (the limit of f exists but isn’t equal to f(a)). So called because you can remove the discontinuity by defining a new function equal to f everywhere except at a, often by factoring a term that goes to 0 at a out of a denominator.

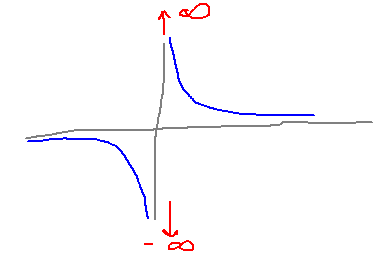
• Discontinuities can be infinite discontinuities (the limit of f from one or both sides is infinite):

• The definition of continuity of f at x = a:
  • f(a) is defined
  • The limit of f(x) as x approaches a exists
  • The limit = f(a).
• The Intermediate Value Theorem: For a continuous f(x) over [a,b], for any y between f(a) and f(b), there is some x = c between a and b, such that f(c) = y.
  • Moreover, this is true for any y between the minimum and maximum values f takes on between a and b (justification: consider f over a new interval defined by the x values at which the minimum and maximum occur).

Justification for the test: suppose there is a horizontal line segment as described in the test, but f is continuous between a and b. Then because the minimum value of f must be below the line, and the maximum above, the Intermediate Value Theorem says there must be some point where f(x) equals the y value of the line segment. But then the segment would intersect f’s graph, which we know it doesn’t. So the only way all the conditions of the test can hold is if f is discontinuous.

But It’s Not a Continuity Test. It’s possible to construct functions that have the property that every horizontal segment passing above some points on the graph and below others intersects the graph, yet the underlying function is not continuous. So failing to satisfy the test does not show that a function is continuous.

Next

Formal definitions of limits

Read section 2.5