Infinite Limits

Return to Course Outline

Previous Lecture

Questions?

Infinite Limits

The “Infinite Limits” subsection of section 2.2.

Examples

Problem. Find lim_x→1- 1/(x-1) and lim_x→1+ 1/(x-1). How about lim_x→1 1/(x-1)²?

Reading ideas: There are 3 kinds of infinite limit, namely ones from the left, ones from the right, and two-sided ones. Each of those 3 kinds is represented in this example.

But what to do with the examples? Maybe start by looking at graphs of the functions to get some intuition for what the limit(s) seem to be. Here’s a graph for 1/(x-1):

It looks like the limit from the left is -∞ and the limit from the right is +∞.

There’s a vertical asymptote, i.e., a vertical line that the function approaches but never reaches, at x = 1.

Use 3 fundamental (but at this point intuitive) rules for infinite limits to confirm these guesses more rigorously:

Problem. Find lim_x→0 (x-1)/(x²-x³).

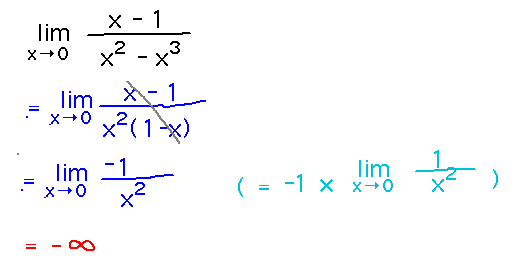
Take-Away. Find an infinite limit by using limit laws or algebra to put the limit expression into one of the fundamental forms. Remember that a in the fundamental forms can be 0, so may not appear explicitly in the expression you’re taking a limit of.

Caution

Infinity is not a number.

Sometimes you can get away with treating it as if it is. For example

• Any real number plus ∞ is infinite
• ∞ + ∞ is infinite
• Any real number times ∞ is infinite.

But sometimes you can’t, for example

• ∞/∞ is not necessarily 1, or even finite
• ∞ - ∞ is not necessarily 0 or finite.

For example, consider subtraction in the context of removing items from infinite sets:

Removing the (infinite number of) integers greater than 2 from the (infinite number of) positive integers leaves you with 2 integers, namely {1,2}. So ∞ - ∞ could be 2.

But you could do a similar thing with the (still infinite number of) integers greater than any finite k to have k integers left. So ∞ - ∞ could be any finite number you like.

And you can even remove an infinite number of integers and still have an infinite number left, for instance remove all the even positive integers to be left with the (infinite number of) odd positive integers. So ∞ - ∞ could be infinity.

Problem. Find lim_x→1+ (x-1) / (x(x-1))

Take-Aways. You can be badly misled by “arithmetic” involving infinity if you aren’t alert to the possible problems. Breaking a fraction into a sum or difference of simpler fractions, as in “Version 2” here, is another useful technique for finding limits though.

Problem Set 2

See handout.

Next

Continuity.

Read section 2.4.

Next Lecture