One-Sided Limits

Questions?

One-Sided Limits

“One-Sided Limits” subsection of section 2.2

Examples

Problem. Find lim_x→2- (x² - 2x) / (x-2) and lim_x→2+ (x² - 2x) / (x-2).

Reading ideas: Limits from left or right are indicated by - or + in limit subscript.

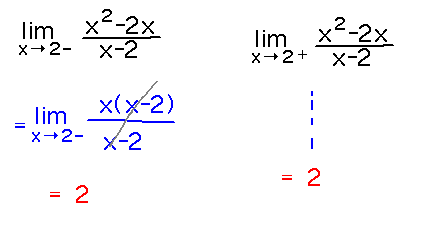
Take-Aways.Limit laws, algebra, etc. work for 1-sided limits as well as 2-sided. 1-sided limits can sometimes be the same as 2-sided (standard) limits.

Problem. Find lim_x→0- (2√x + 1) and lim_x→0+ (2√x + 1).

lim_x→0- (2√x + 1) does not exist because it deals with negative values of x and √x isn’t a real number when x is negative. But lim_x→0+ (2√x + 1) = 1 by plugging in x = 0.

Take-Away.1-sided limits let you talk about limits that don’t exist from both sides, but watch out for the temptation to work on the side where the function values don’t exist.

Problem. Define f(x) by the rules f(x) = x + 1 if x < 0, f(x) = x² + 1 if x ≥ 0. Does lim_x→0 f(x) exist? If so, what is it?

Problem. Define g(x) by the rules g(x) = (x² - 1) / (√x - 1) if x ≤ 1 and g(x) = x² - 1 if x > 1. Show that lim_x→1 g(x) does not exist.

Strategy: Find lim_x→1+ g(x) and lim_x→1- g(x), and show that they are unequal.

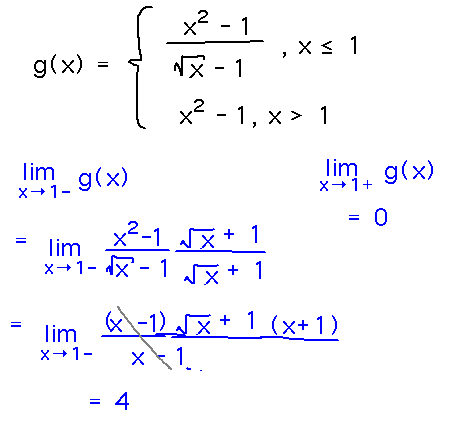
Take-Aways.if left limit = right limit, then both equal the 2-sided limit. Otherwise the 2-sided limit does not exist. One-sided limits are helpful if not essential for dealing with piecewise functions.

Next

Infinite limits

Read the “Infinite Limits” subsection of section 2.2.