SUNY Geneseo Department of Mathematics

Some Limit Laws

Wednesday, September 6

Math 221 05
Fall 2017
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Math Learning Center

Opens today.

Hours are generally

Questions?

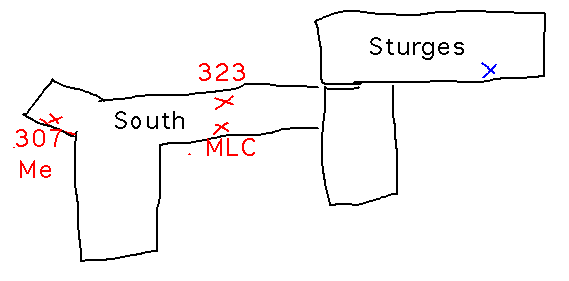
Where Is the Math Department?

On the 3rd floor of South Hall.

Sturges connects to South via Fraser

Homework Question re Limit of 0?

This is a somewhat odd looking application of the law that says any limit of a constant is that constant.

All limits of f(x) = 0 are 0

Using Limit Laws and Algebra

Problem. Use limit laws to confirm Friday’s guess that limx→13x2 = 3.

Reading ideas: The constant multiple and power laws will be helpful here.

Limit as x approaches 1 of 3x^2 breaks down into limit of 3 times limit of x^2 and finally equals 3

Having done this once, you won’t normally have to write out uses of the limit laws in this much detail.

Take-Away. The limit laws let you break down complicated limit expressions into combinations of simpler ones, until (hopefully) you reach simple limits limx→ac or limx→ax.

Problem. Find limx→1(x2 + 2x - 3) / (2x-2).

Reading ideas: Right now the quotient law for limits doesn’t apply because limx→1(2x-2) = 0, so use algebra to simplify the expression until the limit laws do apply.

Factor and cancel to get an evaluable expression

Notice that technically the function we finally took a limit of, (x+3)/2, is not the same function as the one we started with, because (x+3)/2 has one more point in its domain than the original function did.

Problem. Find limx→25(√x - 5) / (x - 25).

Reading ideas. The trick of multiplying by a conjugate to get rid of a square root will help here.

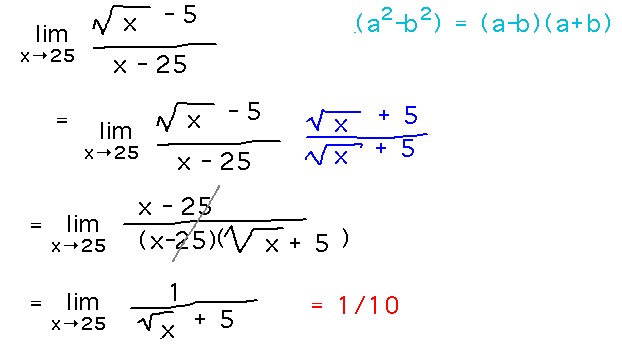
Multiply by (sqrt(x)+5))/(sqrt(x)+5) to cancel out x - 25

Problem. Find limx→0 x / (1+1/x).

Multiply by x/x to cancel out x in 1/x

Take-Aways. Algebraically rewriting limit expressions that can’t be evaluated using the limit laws can sometimes put them into forms that can be evaluated. Factoring to cancel out a problem denominator, and multiplying by a conjugate to remove a square root, are two useful tactics, but not the only ones.

Next

One-sided limits.

Read the “One-Sided Limits” subsection in section 2.2.

Next Lecture